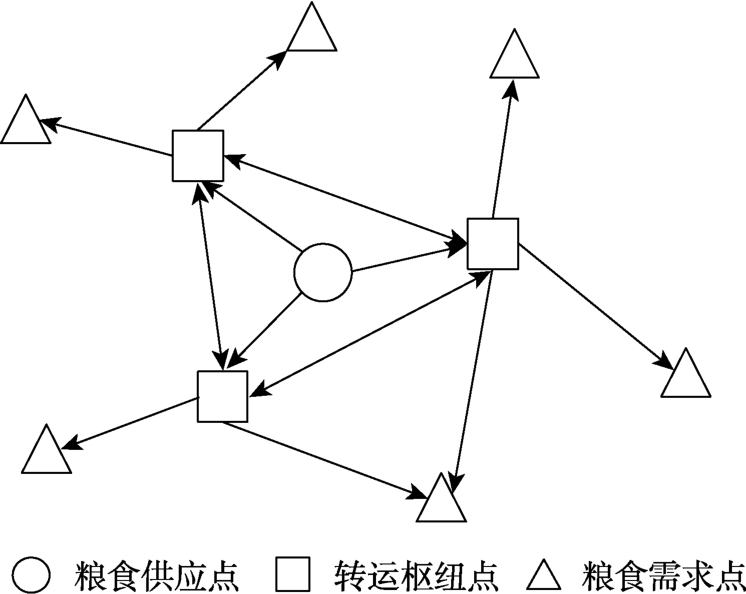
图1 粮食轴辐式网络运输结构
Fig.1 Grain hub-and-spoke network transportation structure
Research on Location and Path Optimization of Grain Transport Hub Driven by Low Carbon
粮食事关国运民生,粮食安全是国家安全的重要基础[1]。目前,中国粮食产量稳步增长,2022年粮食总产量达到68 653 万 t,但随着产量的不断增加,粮食种类及产量供需不平衡、产销地分布不均匀等问题逐渐显著[2]。中国粮食运输网络中大量的供求调运关系集中在较少的地区之间,跨区调粮是中国粮食运输的一大特点[3]。与此同时,随着中国碳达峰、碳中和目标的提出,运输行业在全面绿色低碳转型、优化运输效率等方面愈发受到学者关注[4-5]。在这种背景下,优化粮食转运枢纽及运输路径,既可以实现低碳运输,提高粮食运输效率,又能平衡协调粮食市场,维持粮食市场稳定,是保障中国粮食运输安全的又一重要举措,当前国内外许多学者已对粮食物流行业开展研究。张楷唯等[6]提出应加强铁路粮食物流枢纽节点功能建设、推进粮食多式联运等发展对策,持续发展中国铁路粮食现代物流,王帅等[7]提出了应通过加快铁路、水路基础设施建设、推动粮食物流方式变革等措施,保障粮食的稳定供给和粮食安全。姚海元等[8]总结分析中国粮食专业化码头现状布局情况及存在的问题。Rathore等[9]利用系统动力学方法分析了影响粮食运输的动态反馈效应和风险之间的复杂相互作用。Ndembe 等[10]提出了一种应用在粮食运输行业影子价格方法;轴辐式网络理论的提出[11]和广泛应用[12-13],为粮食运输提高了一种新的研究思路[14-15]。然而,粮食运输作为粮食物流中的一环,专门对其进行的研究较少,且对粮食运输方面的研究较多集中在定性的层面上,主要针对粮食运输发展过程中存在的问题进行分析并提出合理的解决措施,这也是目前研究所存在的问题。
研究选用定量分析的方法,基于轴辐式多式联运网络理论,对中国粮食运输枢纽节点以及路径方案的进行选择;将运输成本,碳排放量作为网络构建的关键影响因素,对比分析是否考虑碳排放的粮食运输方案,建立了以总运输成本最低为目标的粮食转运枢纽选址-路径规划模型,并改进遗传算法对其求解。旨在保障中国粮食运输安全,实现“双碳”目标。
研究所用的轴辐式运输网络结构见图1。现将某批粮食从供应点I 运送到需求点J,途中经过若干个运输节点,节点间的运输路径间存在铁路、水路、公路3 种运输方式,不同运输方式运输时产生的运输费用、运输速度和碳排放量都不同。在考虑各个节点之间调运成本和运输过程中碳排放量都为最低的情况下,同时保障枢纽管辖区域内供求平衡,对转运枢纽进行选址,并对运输路径做出合理规划。为了便于分析问题,现对该模型做出如下假设:

图1 粮食轴辐式网络运输结构
Fig.1 Grain hub-and-spoke network transportation structure
(1)该区域内的粮食流通路径可以直达,也可转运;若不能直达,需经过两个枢纽节点进行转运;
(2)该区域内粮食供应点及粮食转运枢纽不产生粮食需求,且粮食供应点可以满足需求点的需求量;
(3)运输方式为铁路、水路和公路3 种方式联运;
(4)运输过程只与距离和速度有关,不考虑其他情况;
(5)枢纽之间由于规模效应会存在α(0.1)之间的折扣运输;
(6)碳排放量只与粮食运量和距离有关;
(7)不考虑因枢纽转运产生的碳排放成本和运输成本;
(8)该模型的粮食运输仅考虑日常运输,不考虑突发情况下的应急运输。
研究兼顾经济与环境层面,将碳排放量转化为碳排放成本,以粮食运输总成本最小为目标,构建粮食转运枢纽选址及路径优化模型,具体目标函数如下,模型参数及变量说明见表1。
表1 参数及变量说明
Table 1 Parameter and variable description

参数及变量 详细说明N={1,2,3,…n} 区域内所有节点集合,节点个数为n,单位:个P={1,2,3,…p} ∈p N 区域内所有备选粮食转运枢纽节点集合,节点个数为p,单位:个I={1,2,3,…i} ∈i N 粮食的供应节点集合,节点个数为i,单位:个J={1,2,3,…j} j∈N 粮食的需求节点集合,节点个数为j,单位:个K={1,2,3,…k} ∈k P 粮食转运枢纽节点集合,节点个数为k,单位:个M={1,2,3} ∈m N 节点之间的运输方式集合,运输方式共3 种Qij 供应节点i 到需求节点j 的粮食运输量,单位:t Qi 节点i 的粮食产量,单位:t Ck 单个粮食中转库枢纽的建设成本,单位:万元Cmij 选择第m 种运输方式从节点i 到节点j 的单位运输费用,单位:元/吨千米Dij 两节点之间的直线距离,单位:km α 枢纽点之间因规模效应产生的运输成本折扣因子,0≤α≤1 β β 为人均粮食消耗量Hi 节点i 所在区域的人口数etm 第m 种运输方式的单位碳排放量,单位:kg/t·km γ 碳税,单位:元/t Xik={0,1} 决策变量,若节点i 与枢纽k 直接相连,则Xik=1,否则Xik=0 Xij={0,1} 决策变量,若节点i 与节点j 之间存在直达路线,则Xij=1,否则Xij=0 Yk={0,1} 决策变量,若节点i 选为枢纽节点,则Yk=1,否则Yk=0
碳排放成本ZC 由运输过程中的距离和运输量决定,因此其计算公式为:
若供应点i 到需求点j 存在直达的运输方式,即运输过程中不存在粮食转运,则粮食运输成本的目标函数为:
其中:
若供应点i 到需求点j 直接不存在直达路线,即运输过程中需要经过转运枢纽,则粮食运输需要通过三个阶段。
第一个阶段为供应点i 到枢纽点k,该阶段的运输成本为:
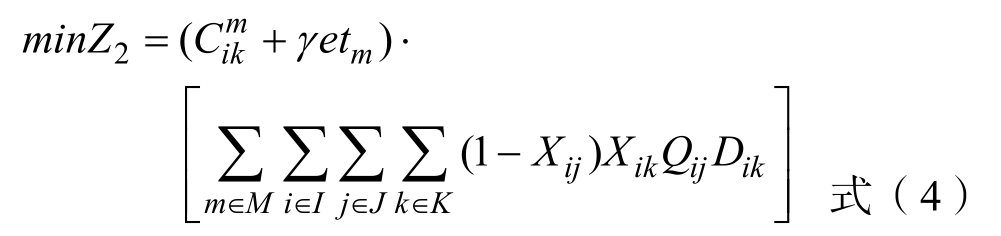
第二阶段为枢纽点k 到枢纽点g,该阶段的运输成本为:
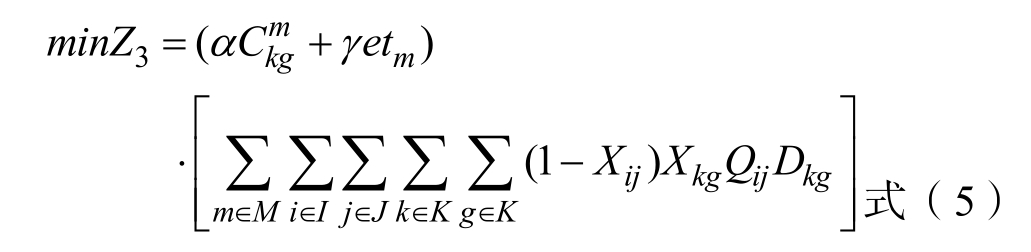
第三阶段为枢纽点g 到需求点j,该阶段的运输成本为:
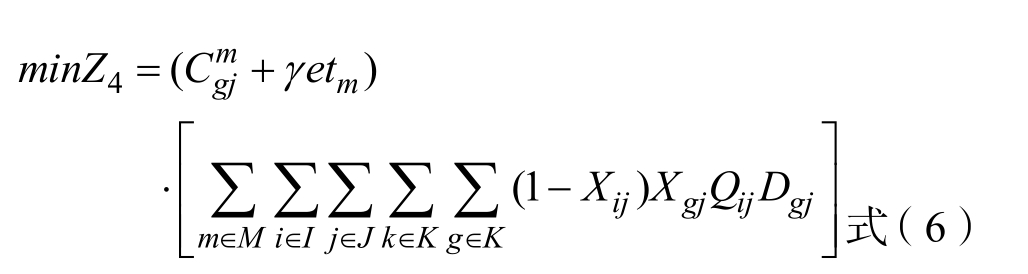
粮食转运枢纽的建设费用为:
故最终的目标函数模型为:
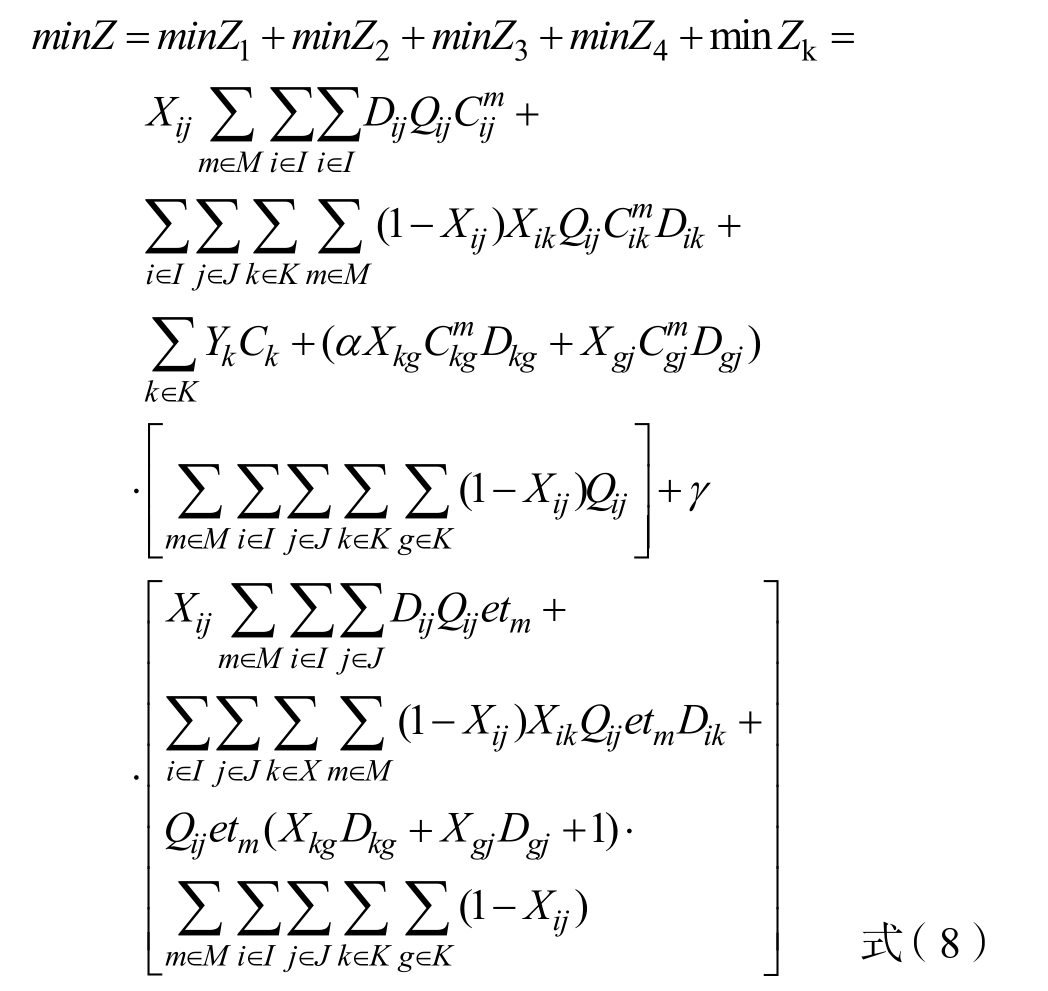
约束条件:
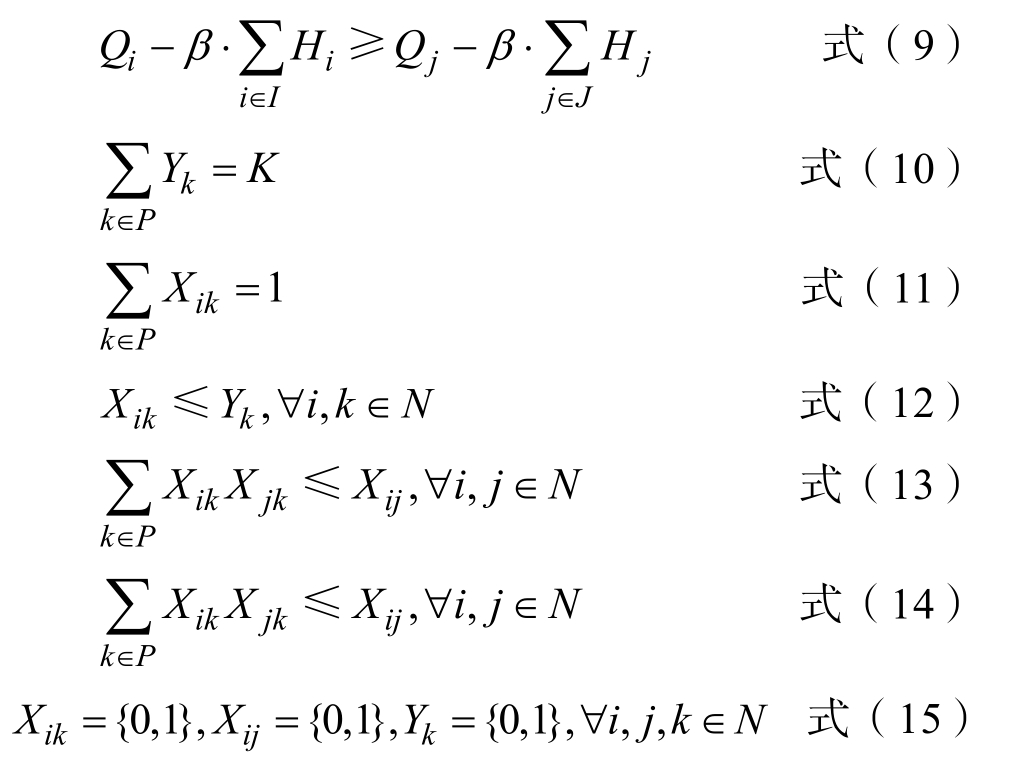
式(9)表示粮食供需平衡条件,粮食调运是在保障该区域粮食需求得到满足的条件下进行的,若某区域粮食并未实现自给,则将其从备选枢纽节点中移除。式(10)表示整个轴辐式多式联运网络中枢纽点的数量是k 个,式(11)(12)(13)表示一个非枢纽节点只能与一个枢纽节点相连接,式(14)表示不同节点之间可以存在直达路径,但连接不同枢纽节点的非枢纽节点之间不存在直达路径,式(15)表示决策变量。
实际生活中粮食运输网络构成的轴辐式网络较为复杂,求解规模较大,精确算法难以得到最优解,因此研究选用启发式算法——改进遗传算法进行求解。研究将自适应与模拟退火策略与遗传算法结合,设计出适用于实际生活的粮食低碳运输选址-路径模型的求解算法,算法流程见图2 所示。

图2 改进遗传算法流程图
Fig.2 Flow chart of improved genetic algorithm
在国家发展改革委、国家粮食局发布的《粮食物流业“十三五”发展规划》中,为促进粮食物流系统化发展,围绕中国发展战略,重点完善和发展“两横、六纵”8 条粮食物流重点线路,重点布局50 个左右一级节点,110 个左右二级节点[16]。
研究以上述8 条粮食物流重点线路和重要节点为切入点,结合各地区粮食运输实际情况,进行粮食低碳运输网络优化研究。为便于计算,将网络节点定位于各省省会城市,节点坐标为其对应的各省会城市的经纬度坐标。并计算出各省份粮食余量,粮食余量分布见图3。基于各省粮食余量及现有的8 条粮食物流重点线路,研究共筛选出5 个粮食供应点、9 个备选枢纽点、11 个粮食需求点为研究对象。网络节点属性及编号见表2 所示。各省会城市之间选用铁路、水路、公路3种运输方式混合运输,运输距离取实际运输距离,数据来自实地考察。
表2 节点属性及编号
Table 2 Node attributes and numbers
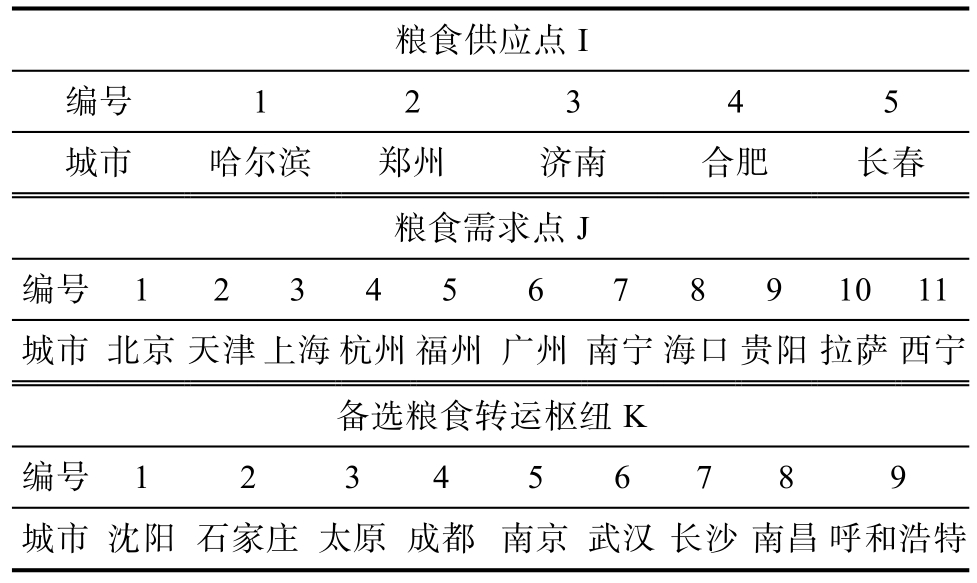
粮食供应点I编号 1 2 3 4 5城市 哈尔滨 郑州 济南 合肥 长春粮食需求点J编号 1 2 3 4 5 6 7 8 9 10 11城市 北京 天津 上海 杭州 福州 广州 南宁 海口 贵阳拉萨西宁备选粮食转运枢纽K编号 1 2 3 4 5 6 7 8 9城市 沈阳 石家庄 太原 成都 南京 武汉 长沙 南昌呼和浩特
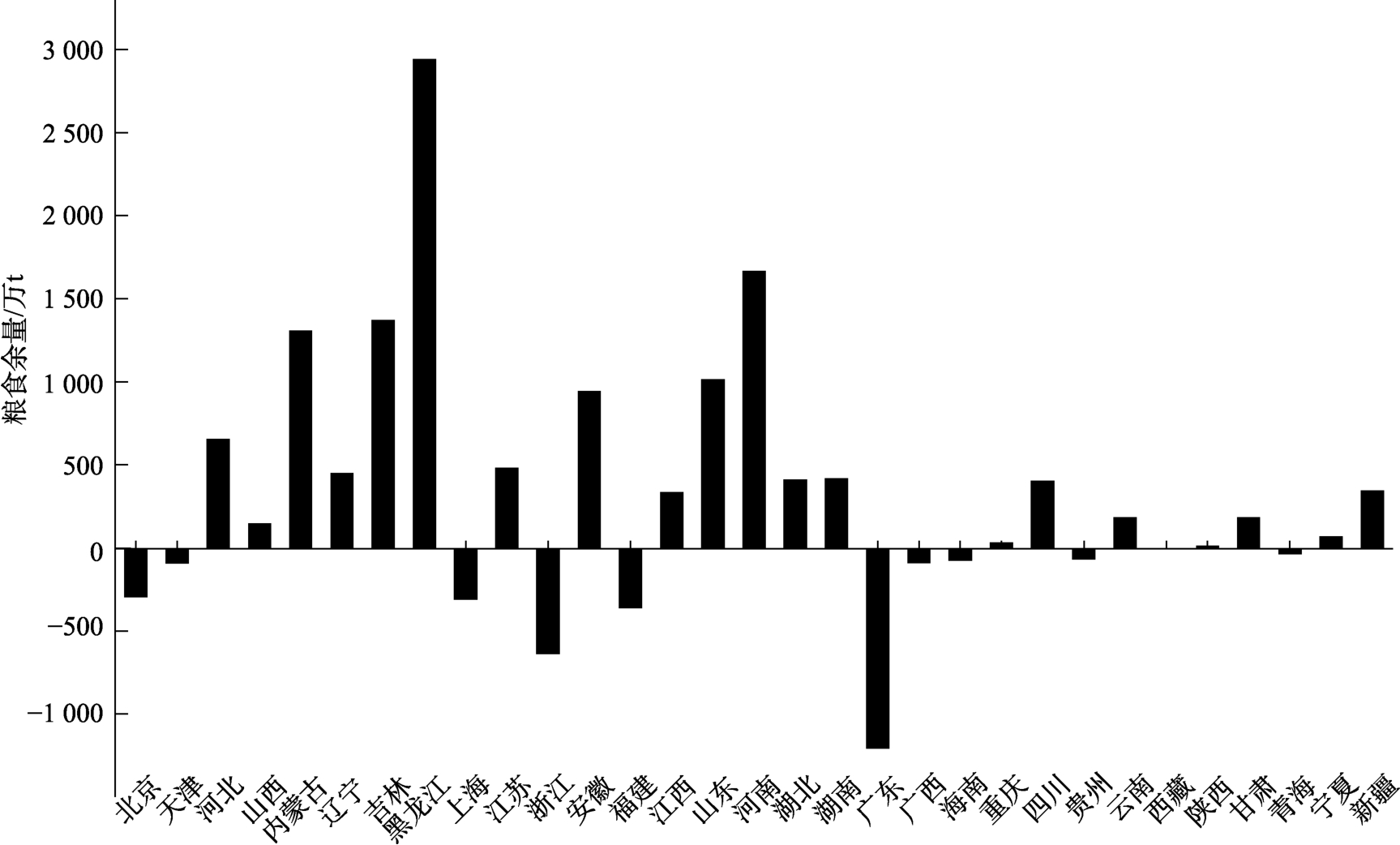
图3 中国部分省份粮食余量
Fig.3 Grain surplus in some provinces of China
粮食产量、人均粮食消费量、人口数量等数据均来自《2022 年中国统计年鉴》,运输过程中二氧化碳排放因子来自IPCC 公布的数据。财政部建议到2020 年,碳税的税率可提高到40 元/t。而环保部规划院课题组则建议,到2020 年可以征收50 元/t,因此碳税取均值45 元/t。我国公路、水路运价机制相对灵活,随市场需求波动明显[17],公路及水路运输价格均来自实地考察,铁路运输价格来自《铁路货物运价规则》其他具体参数设置及数据信息见表3。
表3 模型参数设置
Table 3 Model parameter settings
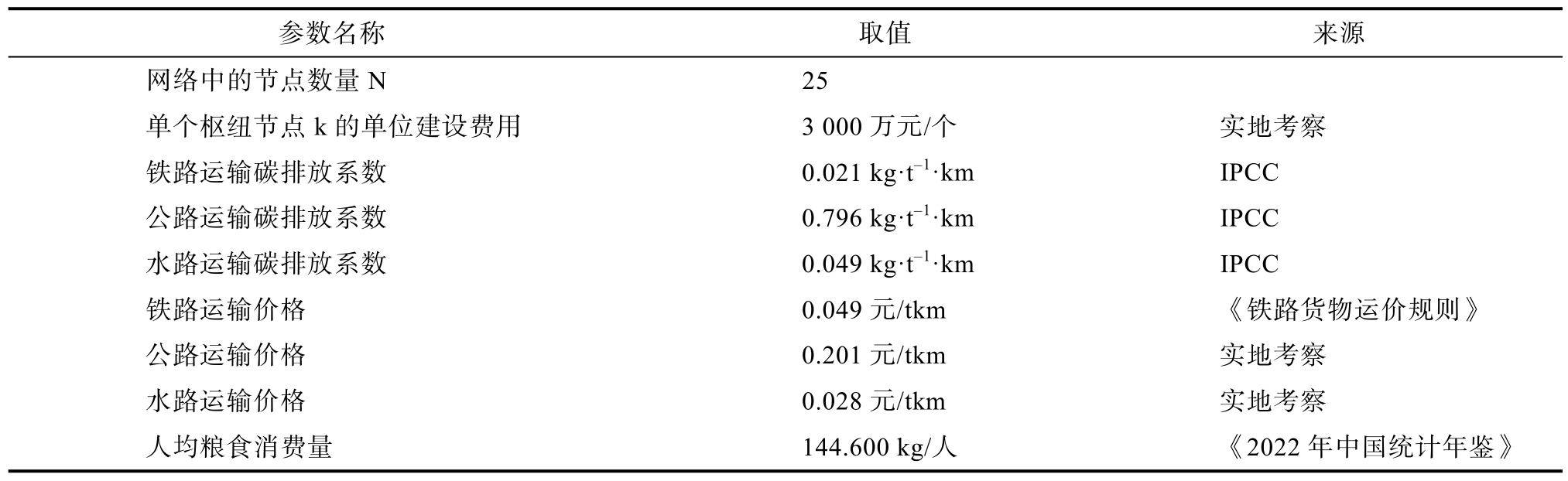
参数名称 取值 来源网络中的节点数量N 25单个枢纽节点k 的单位建设费用 3 000 万元/个 实地考察铁路运输碳排放系数 0.021 kg·t-1·km IPCC公路运输碳排放系数 0.796 kg·t-1·km IPCC水路运输碳排放系数 0.049 kg·t-1·km IPCC铁路运输价格 0.049 元/tkm 《铁路货物运价规则》公路运输价格 0.201 元/tkm 实地考察水路运输价格 0.028 元/tkm 实地考察人均粮食消费量 144.600 kg/人 《2022 年中国统计年鉴》
基于以上算法设计和算例,将改进遗传算法参数设置为:种群规模100,最大迭代次数200,初始温度T0500,退火系数0.95。求解算例获得最优目标的迭代情况见图4,可知:算法前30 次迭代快速收敛,随后收敛速度减缓,并在60 次左右产生最优解,整体体现出较好的收敛性。
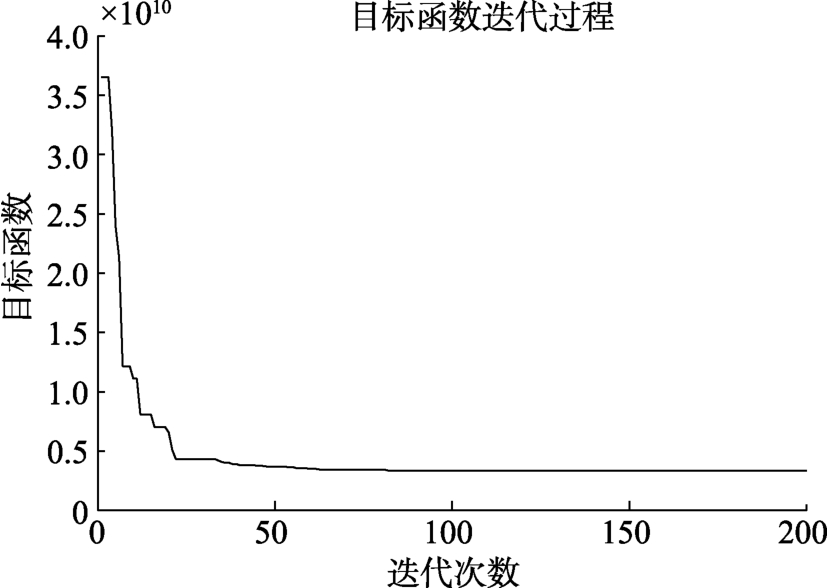
图4 算法迭代结果
Fig.4 Algorithm iteration results
通过改进遗传算法求解该算例,获得的最优目标函数值包括总运输成本、碳排放成本、直达运输成本、不同转运阶段运输成本和枢纽节点建设成本,具体结果见表4。
表4 算法求解结果
Table 4 Algorithm solution results
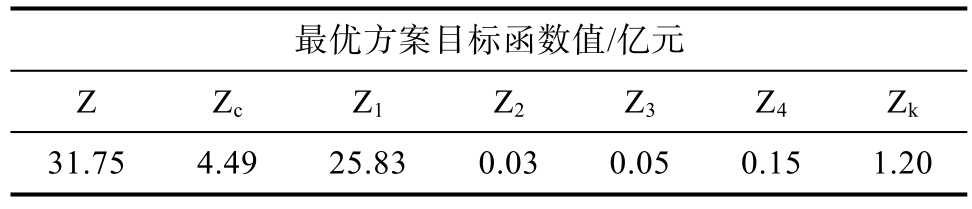
最优方案目标函数值/亿元Z Zc Z1 Z2 Z3 Z4 Zk 31.754.4925.830.03 0.05 0.151.20
不同情况下粮食运输方案对比见表5,包括枢纽选址方案、运输线路方案、各运输路段之间的运输方式以及总运输成本,具体方案为从备选枢纽中选取石家庄、南京、长沙、南昌为粮食转运枢纽。
表5 不同情况下粮食运输方案对比
Table 5 Comparison of grain transport schemes under different conditions

不考虑碳排放的粮食运输方案 考虑碳排放的粮食运输方案枢纽选择 运输路径 运输方式 枢纽选择 运输路径 运输方式[3,1] [1] [1,1] [1][3,2] [1] [5,2] [1][2,3] [1] [4,3] [1][4,4] [1] [4,4] [1][3,5,8,5] [2,1,1] [4,5,8,5] [2,1,1][2,6,7,6] [1,2,1] [5,2,7,6] [3,2,2][5,7] [1] [5,2,7,7] [1,1,1][3,2,7,8] [1,1,1] [4,5,7,8] [2,1,1][4,5,7,9] [2,1,1] [3,2,7,9] [2,1,1][4,5,3,10] [2,1,1] [4,5,7,10] [2,2,1]2、3、5、6、7、8[3,2,3,11] [1,1,1]2、5、7、8[2,11] [1]总运输成本/万元 368 693.56 总运输成本/万元 317 531.84
不同枢纽节点数目对应的各项成本见图5,从中可以看出,当设置4 个枢纽节点时,总运输成本和碳排放成本均达到最小,能够实现规模效应。
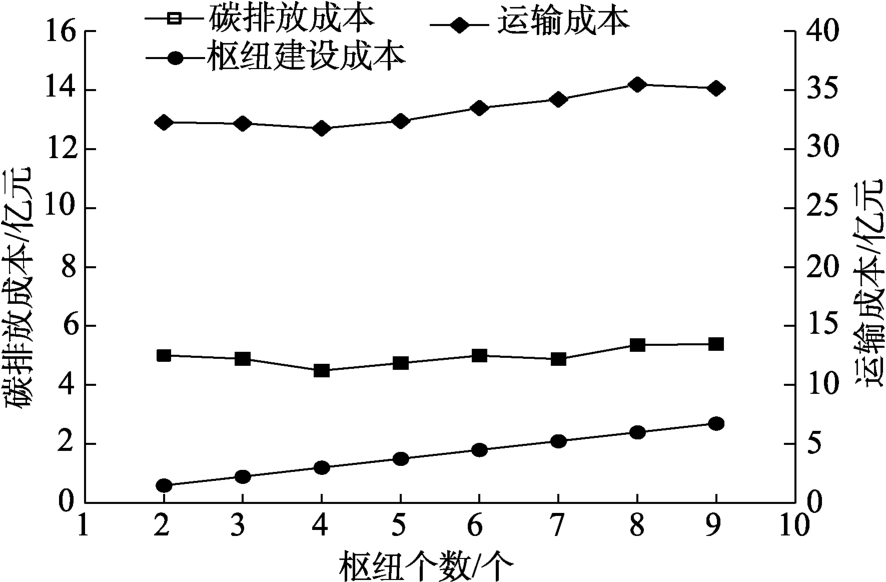
图5 不同枢纽不同枢纽数目下的成本
Fig.5 Cost under different number of hubs
从运输网络结构看,不论是原方案还是优化后的方案,都较多的采用了铁路运输,究其原因,可能是在粮食跨省调运过程中,水路运输虽具有较多优势,但其主要针对我国沿海地区及粮食进出口运输,受地理因素影响较大;而公路运输虽灵活性较高,但其运输成本及运输碳排放量均较高,因此在粮食跨省调运过程中,铁路运输占比较高。原运输方案选择了石家庄、太原、南京、武汉、长沙、南昌六个粮食转运枢纽,基于提出的考虑碳排放的粮食运输模型优化后,关闭了太原、武汉枢纽,碳排放量减少了10.23%,平均枢纽转运能力提升了9.63%。不同运输方案下枢纽转运量对比见表6 所示:原运输网络枢纽选址较为密集,粮食转运任务基本集中在武汉、长沙等长江沿岸地区,且枢纽点之间距离较近,在远距离跨省运输过程中未能体现出枢纽间转运的折扣效应,造成运输成本增加;且原运输方案选取的6 个粮食转运枢纽转运量过剩,如太原等地,粮食转运量不足5.00%。一方面由于当前经过该枢纽的运输量未达到饱和,导致资源过剩,一定程度上增加了运输成本、枢纽的建设及维护成本和运输的碳排放量;另一方面,枢纽转运量过剩直接导致枢纽的转运价值降低;优化后的粮食运输网络中,减少两个粮食转运枢纽,重新分配粮食转运量,枢纽的平均饱和度提升为28.02%。如石家庄这一转运枢纽,优化后的饱和度为41.23%,该枢纽主要承担东北地区的粮食转运任务,增加该枢纽的转运量,不仅能够满足所需城市的粮食供应运输任务,维持粮食北粮南运的调运平衡,简化粮食运输路线,而且具有远距离运输折扣规模效应,节约运输成本。枢纽节点数量减少两个后,粮食的转运成本、枢纽节点的建设成本以及后续维护成本减少了13.87%,枢纽的转运效率明显提高。
表6 不同运输方案下枢纽转运量对比
Table 6 Comparison of hub transshipment volume under different transportation schemes 1×108t
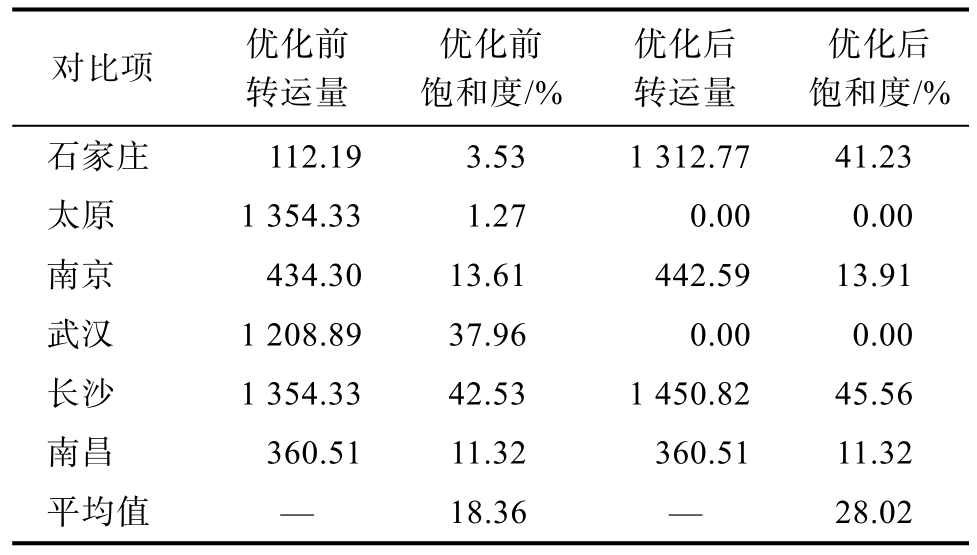
对比项 优化前转运量优化前饱和度/%优化后转运量优化后饱和度/%石家庄 112.19 3.53 1 312.77 41.23太原 1 354.33 1.27 0.00 0.00南京 434.30 13.61 442.59 13.91武汉 1 208.89 37.96 0.00 0.00长沙 1 354.33 42.53 1 450.82 45.56南昌 360.51 11.32 360.51 11.32平均值 — 18.36 — 28.02
从运输路径来看,优化后网络与原网络主要区别在于:考虑了运输过程中的碳排放量,较多的选用了多式联运,同时降低了成本。不同运输方式的特点不同,将3 种运输方式联合考虑,能够使碳排放量减少到最低,如原运输方案为{[5,7],[1]},表示将粮食由铁路从长春直接运输到南宁,而考虑碳排放后的运输方案为{[5,1,7,7],[1,1,1]},表示由铁路将粮食运输到沈阳,沈阳再运输到长沙,最后由长沙运输到南宁。通过转运,运输距离比同样采用铁路方式从长春到南宁直达可节约277 km,碳排放量减少了10.24%,且由于存在枢纽间的大宗货物折扣系数,运输价格也降低了37.81%。因此,允许转运的网络更符合实际需求,更具有经济性。根据运输方案也可得出,公路运输在粮食跨省运输中优势并不明显。
为验证设计的改进遗传算法求解的有效性和适用性,以研究所用实际数据为例,将改进遗传算法、传统遗传算法和粒子群算法进行对比。设置粒子群算法的粒子数 N 为 20,加速系数c1=c2=1.5,惯性权重Wmax=1,Wmin=-1,最大迭代次数为200。3 种求解结果对比见表7,根据该表可以观察到,改进遗传算法从综合方面考虑优于其他两种算法,得到的目标函数值结果最小,迭代次数和运行时间较快,结果稳定,更适用于粮食运输选址-路径研究。
表7 不同求解算法结果对比
Table 7 Comparison of results of different solving algorithms
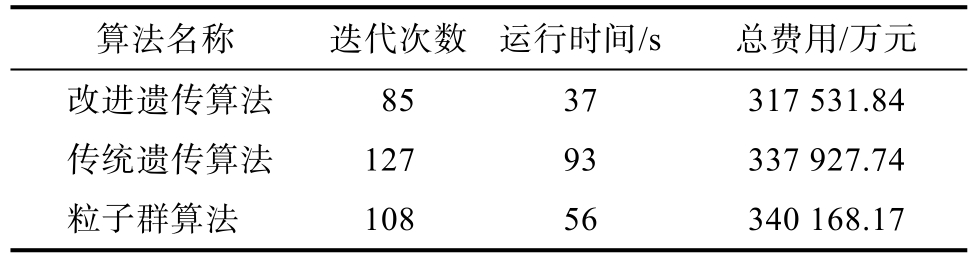
算法名称 迭代次数 运行时间/s 总费用/万元改进遗传算法 85 37 317 531.84传统遗传算法 127 93 337 927.74粒子群算法 108 56 340 168.17
文章基于已有的粮食运输网络布局,构建了考虑粮食运输过程中碳排放量的轴辐式多式联运网络枢纽节点选址-路径优化模型及算法,并对是否考虑碳排放的粮食运输方案进行对比分析。研究结果如下:
(1)为使中国粮食运输网络总运输成本和碳排放量最小,应该选取石家庄、南京、长沙、南昌作为枢纽节点,其他运输节点与以上枢纽合理连接,能够使运输成本减少13.87%、碳排放量减少10.23%,枢纽平均转运效率提升9.66%。
(2)该模型及算法能够适用于低碳驱动下中国实际粮食运输过程,对解决实际问题具有可行性。
[1] 《中国的粮食安全》白皮书(全文)[J]. 黑龙江粮食, 2019,198(11): 40-47.《White Paper on Food Security in China》(Full Text)[J].Heilongjiang Grain, 2019, 198(11): 40-47.
[2] 普蓂喆, 周琳, 钟钰, 等. 中国粮食产销平衡区和主销区粮食自给底线设定研究[J]. 农业经济问题, 2022, 511(7): 113-123.PU M Z, ZHOU L, ZHONG Y, et al. Setting bottom lines for grain self-sufficiency in the grain production-and-consumingbalancing areas and major grain-consuming areas in China[J].Issues in Agricultural Economy, 2022, 511(7): 113-123.
[3] 向长琼, 周浩, 张华昌, 等. “北粮南运”散粮集装箱储运建设的思考[J]. 粮油仓储科技通讯, 2018, 34(6): 1-2+11.XIANG C Q, ZHOU H, ZHANG H C, et al. Thinking on the Construction of Bulk Grain Container Storage and Transportation of “Northern Grain to the South”[J]. Grain and oil storage technology newsletter, 2018, 34(6): 1-2+11.
[4] 李慧芳, 胡大伟, 陈希琼, 等. 考虑碳排放的混合轴辐式多式联运网络枢纽扩增选址-路径问题[J]. 交通运输工程学报,2022, 22(4): 306-321.LI H F, HU D W, CHEN X Q, et al. Expanding hub location-routing problem for hybrid hub-and-spoke multimodal transport network considering carbon emissions[J]. Journal of Traffic and Transportation Engineering, 2022, 22(4): 306-321.
[5] 张建军, 王嘉铭, 王天浩, 等. 低碳情景下的复合轴辐式快递网络规划[J]. 同济大学学报(自然科学版), 2023, 51(2):288-294.ZHANG J J, WANG J M, WANG T H, et al. Multi-layered multi-service-leveled hybrid hub-spoke network design in low-carbon scenarios[J]. Journal of Tongji University(Natural Science), 2023, 51(2): 288-294.
[6] 张楷唯, 张巍, 刘畅. 中国铁路粮食物流发展对策探讨[J]. 铁道货运, 2018, 36(12): 36-41.ZHANG K W, ZHANG W, LIU C. A study on the strategies to promote railway food logistics in China[J]. Railway Freight Transport, 2018, 36(12): 36-41.
[7] 王帅, 赵秀梅. 中国粮食流通与粮食安全: 关键节点的风险识别[J]. 西北农林科技大学学报(社会科学版), 2019, 19(2):124-132.WANG S, ZHAO X M. Grain circulation and food security:based on risk identification in key nodes[J]. Journal of Northwest A& F University(Social Science Edition), 2019, 19(2):124-132.
[8] 姚海元, 王达川, 丁文涛, 等. 中国沿海粮食运输系统与粮食专业化码头布局分析[J]. 水运工程, 2021, 585(8): 36-41.YAO H Y, WANG D C, DING W T, et al. Planning of China’s coastal grain transportation system and layout of specialized grain wharf[J]. Port & Waterway Engineering, 2021,585(8): 36-41.
[9] RISHABH R, THAKKAR J J, JHA J K. Impact of risks in foodgrains transportation system: a system dynamics approach[J]. International Journal of Production Research, 2021, 59(6):1814-1833.
[10] ELVIS N, BITZAN J D. A shadow price approach examining service quality in a heavily captive U.S. freight transportation market: the case of grain transport[J]. Transport Policy, 2022,1161-10.
[11] O'KELLY E M. The location of interacting hub facilities[J].Transportation Science, 1986, 20(2).
[12] 王帮俊, 赵伟, 朱伟. 考虑拥堵和容量限制的多式联运轴辐式物流网络布局优化研究[J]. 工业工程与管理, 2022, 27(1):65-73.WANG B J, ZHAO W, ZHU W. Research on layout optimization of multi-modal hub and spoke logistics network considering congestion and capacity limitation[J]. Industrial Engineering and Management, 2022, 27(1): 65-73.
[13] RICHARD K, RICO M, ORIOL L. Mesh network as a competitive advantage for European LCCs: An alternative topology to hub-and-spoke for selling online connections[J].Transport Policy, 2021, 106196-204.
[14] 李凤廷, 侯云先. 轴辐式粮食物流网络的横向协同: 一个整合的概念框架[J]. 农业经济问题, 2014, 35(3): 75-83+112.LI F T, HOU Y X. Horizontal collaboration for hub-and-spoke system in grain industry: a conceptual framework[J]. Issues in Agricultural Economy, 2014, 35(3): 75-83+112.
[15] 邓红星, 周洁, 胡翼. 考虑碳排放的生鲜农产品冷链物流配送路径优化模型[J]. 重庆理工大学学报(自然科学), 2023,37(2): 289-297.DENG H X, ZHOU J, HU Y. Optimization model of the cold chain logistics distribution path of fresh agricultural products considering carbon emission[J]. Journal of Chongqing University of Technology(Natural Science), 2023, 37(2): 289-297.
[16] 国家发展改革委, 国家粮食局《粮食物流业“十三五”发展规划》[EB/OL]. [2017-03-03]. http://www.gov.cn.The National Development and Reform Commission, State Administration of Grain. 《The ‘13th Five-Year’ Development Plan of Grain Logistics Industry》[EB/OL]. [2017-03-03].http://www.gov.cn.
[17] 武慧荣, 陈少阳, 崔淑华. 基于熵权TOPSIS 模型的大宗货物运输方式综合评价[J]. 重庆理工大学学报(自然科学), 2022,36(6): 254-260.WU H R, CHEN S Y, CUI S H. Evaluation of bulk goods transportation mode based on entropy TOPSIS method[J].Journal of Chongqing University of Technology (Natural Science), 2022, 36(6): 254-260.