我国是人口大国,粮食安全是国家安全的重要一项,储粮安全便显得尤为重要,而我国国家级储粮方式以大型房式仓储粮方式为主。此种方式无论是长期存放还是定期通风,作为研究对象的多孔介质粮堆的渗流特性都将是研究的重点,其中粮堆的渗透率与粮堆的温度水分分布和通风效果密切相关,研究表明多孔介质的孔隙率是渗透率的单值函数,孔隙率可以用来确定非固结颗粒渗透率[1]。粮堆形成的结构为多孔介质形式,此种空隙结构较复杂,研究发现实际多孔介质在一定尺度范围内具有分形的特征,且在自然储粮过程中由于环境温度等因素的变化产生的温度梯度导致的微气流流动较为缓慢,且通风过程中粮堆内气流为层流状态[2-3],使得分形理论用于此研究成为一种可能。
研究发现[4],多孔介质的分形维数越大,渗透率越大,研究多孔介质的分形维数对于多孔介质来说很重要。随着科技的进步[5],使用软件模拟来保障粮食安全越来越受到人们的关注,桂便等[6]曾探索卷积神经网络用于识别粮堆中害虫,减少粮食的虫害问题。本研究将从粮堆渗透率影响因素入手,使用盒维数法来探究粮堆入库速度和堆积方式对于粮堆分形维数和渗透率的影响,为粮食合理入库、保护粮食安全提供帮助。
1 分形多孔介质分形维数与孔隙率和渗透率的相互关系
1.1 分形维数对孔隙率的影响
分形多孔介质孔隙分形维数D是定量表征多孔介质内部不规则微观结构特性的参数,数学表达式为:
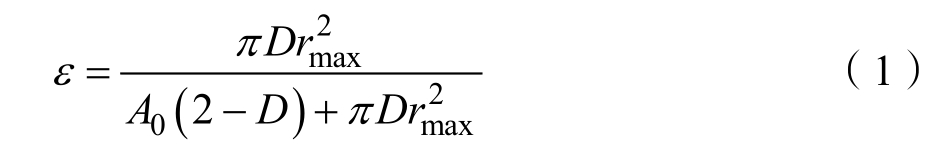
式中D为孔隙分形维数,rmax为最大孔隙半径,m,A0为截面面积,m2,ε为孔隙率。
由数学表达式可知多孔介质孔隙率随孔隙分形维数的增加而呈递增的趋势。
1.2 分形维数对渗透率的影响
由李瑞川[4]的研究可知分形维数与渗透率的数学表达式为:

式中K为渗透率,ω为迂曲度。
迂曲度ω一般可用以下数学关系式表示:
式中a>0为经验常数,取0.74。
由数学表达式可知多孔介质渗透率随孔隙分形维数的增加而呈递增的趋势。
由此可知研究粮堆的孔隙分形维数对于粮堆的存放和后续的通风经济性考虑都有重要作用,粮堆的渗透率较大时,有利于粮堆温度的控制和机械通风时能耗的减小。因而研究影响粮堆的分形维数大小的因素也就尤为重要,本文将就此展开研究与讨论。
2 盒维数法介绍
为了定量地描述客观事物的“非规则”程度,德国数学家豪斯多夫在1918年引入了维数的概念。不同方法测出来的维数名称也不同,其中盒维数法是最常用的测分形维数方法之一,方便数学计算和经验估计[7]。
2.1 盒维数的定义
假设分形物体为G,D是计盒维数,N(δ)是边长δ的盒子可以覆盖G的数目,物体的计盒维数D数学表达式如下:
实际计算时,为求出由上式定义的盒维数,可由如下方式得到:
(1)用边长为δ的小正方形覆盖物体G,N(δ)为覆盖个数;
(2)取不同的边长δ值,将会得到不同的覆盖数目N(δ),记录所有数据;
(3)分别对δ和N(δ)取对数,得到ln(δ)和lnN(δ),在对数坐标系上绘制统计曲线;
(4)选取近似直线的有效点,计算曲线斜率,斜率的负数即为所要求的计盒维数D。
盒维数的计算较为简单,可通过计算机编程得到,因此此方法的应用十分广泛,如纺织图案、岩石结构、土壤和自然堆积谷物等分形的分维计算。图2.1为一纺织图案盒维数测量[8]。
2.2 二值法盒维数的计算
二值法[9-11]是以黑白位图为研究对象,其计算基本思想简单,在计算盒维数中应用广泛。首先,对图形文件作预处理,得到黑白位图,并转化为像素矩阵,在像素矩阵中黑色点用1表示,白色点用0表示;然后将像素矩阵逐次n等分,得到含有元素1的单元格,并计算单元格中非零矩阵的个数;接着,在双对数坐标系下对计盒尺寸和对应尺寸下非零矩阵的个数进行线性回归分析拟合,如果线性相关,得到的直线的斜率即为所求的计盒维数。二值法流程图如下图2.2。
图1 一纺织图案盒维数测量
Fig.1 Dimension measurement of a textile pattern box

图2 二值法流程图
Fig.2 Flow chart of binary method
3 验证盒维数计算程序的准确性
为了验证盒维数计算程序的准确性,本文首先对点图、线性图、平面图、Koch雪花和Sierpinski垫片结构进行了盒维数计算验证。验证结果如表3.1,由结果可知误差较小,本文计算程序是合理有效的。
表1 多种分形图像盒维数计算结果
Table 1 Calculation results of box dimension of various fractal images
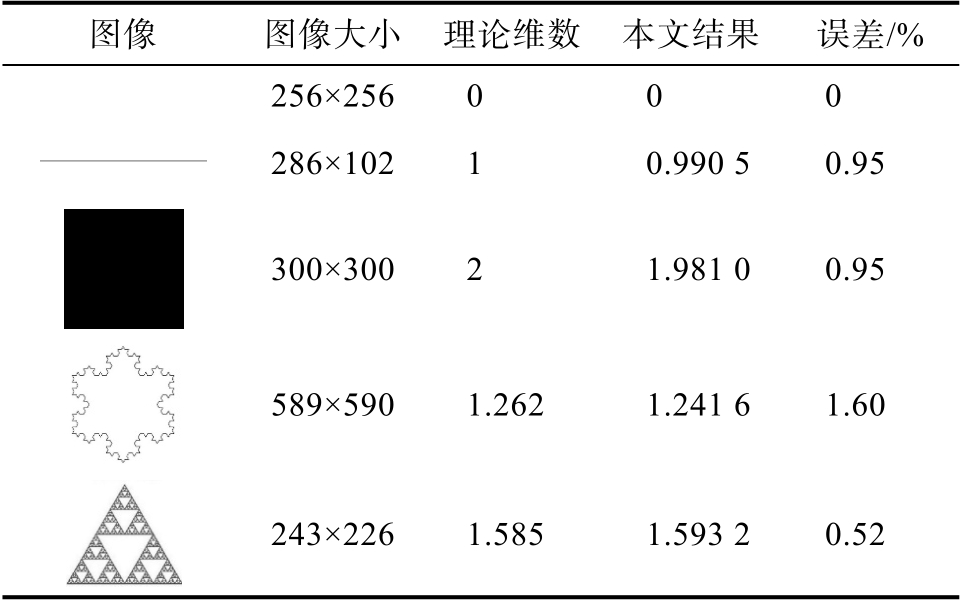
图像 图像大小理论维数 本文结果 误差/%256×2560 0 0images/BZ_210_1323_1071_1488_1130.png286×1021 0.990 5 0.95images/BZ_210_1347_1147_1465_1265.png300×3002 1.981 0 0.95images/BZ_210_1347_1282_1465_1401.png589×5901.262 1.241 6 1.60images/BZ_210_1348_1418_1463_1524.png243×2261.585 1.593 2 0.52
4 EDEM模拟堆粮
本研究以稻谷为研究对象。
4.1 稻谷颗粒填充
稻谷的实际尺寸近似椭球,本研究以长轴为9 mm,短轴为2 mm的椭球为稻谷颗粒模型,并以此为基础在EDEM中进行填充,填充而成的稻谷如图3。

图3 稻谷颗粒填充
Fig.3 Rice grain filling
4.2 稻谷模拟入库速度确定
稻谷的密度为1 020~1 210 kg/m3,本文选取密度为1 040 kg/m3,计算得到稻谷颗粒每个质量1.66×10-5 kg,大型房式仓实际堆粮过程粮食入库速度为50~200 t/h,为多个运粮机共同工作。单个运粮机皮带输送速度为1~40 t/h,即粮食入库速度为1.6×104~6.69×105个/s。
本文研究对象为长29.5 m,宽17.5 m,装粮线高5 m的房式仓。模拟粮仓为缩放模型,粮仓模型底部长59 mm,宽35 mm,颗粒工厂位于模型上方,长50 mm,宽30 mm。实际堆粮过程稻谷经过运粮机入库形成的粮柱截面约为长0.6 m,宽0.2 m的长方形。粮食工厂生成稻谷颗粒速度为:
改变颗粒工厂生成粮食颗粒数的速度,本文选取五组数据分别为5 000、4 000、3 000、2 000、1 000 个/s。以速度5 000 个/s时为例,模拟稻谷堆积情况如图4。

图4 5 000个/s时稻谷堆积情况
Fig.4 Rice accumulation at 5 000/s
4.3 稻谷堆积方式确定
由于粮食颗粒较为均匀,大小多为图3所示的稻谷颗粒大小,但在稻谷生长和收割运输过程中,自然生长或人为原因会产生少量的小颗粒稻谷。为了简化模型,小颗粒稻谷也使用椭球模型,长轴和短轴取图3大颗粒的一半,长轴为4.5 mm,短轴为1 mm。稻谷总数取2 500 个,大小颗粒各取1 250 个,小颗粒体积较小实际占有体积与大颗粒相比较小,符合实际情况。颗粒工厂生成速度取5 000 个/s。
为了研究将稻谷颗粒分拣开后分层堆积是否能够增加粮堆分形维数和渗透率,将分三种堆积情况进行模拟研究,分别为大小颗粒混合堆积即粮堆自然堆积、大小颗粒分层堆积和大小颗粒分成四层堆积,以稻谷大小颗粒分成四层为例,如图5为堆积情况(大颗粒为黑色,小颗粒为灰色)。

图5 稻谷粮堆大小颗粒四层堆积情况
Fig.5 Four layer accumulation of large and small particles in rice grain pile
5 粮食的入库速度对分形维数的影响
对于粮食的入库速度对分形维数的影响研究,同时要考虑到粮食入库的效率问题,以期找到合理的粮食入库速度,指导实际粮食的入库。五组数据分别为5 000、4 000、3 000、2 000、1 000个/s,由于粮堆分布较为均匀,沿宽度方向孔隙率和渗透率差别不大,本文选取稻谷堆宽度方向中间位置截面图来研究,截面图和相应计算的分形维数和孔隙率如下图。
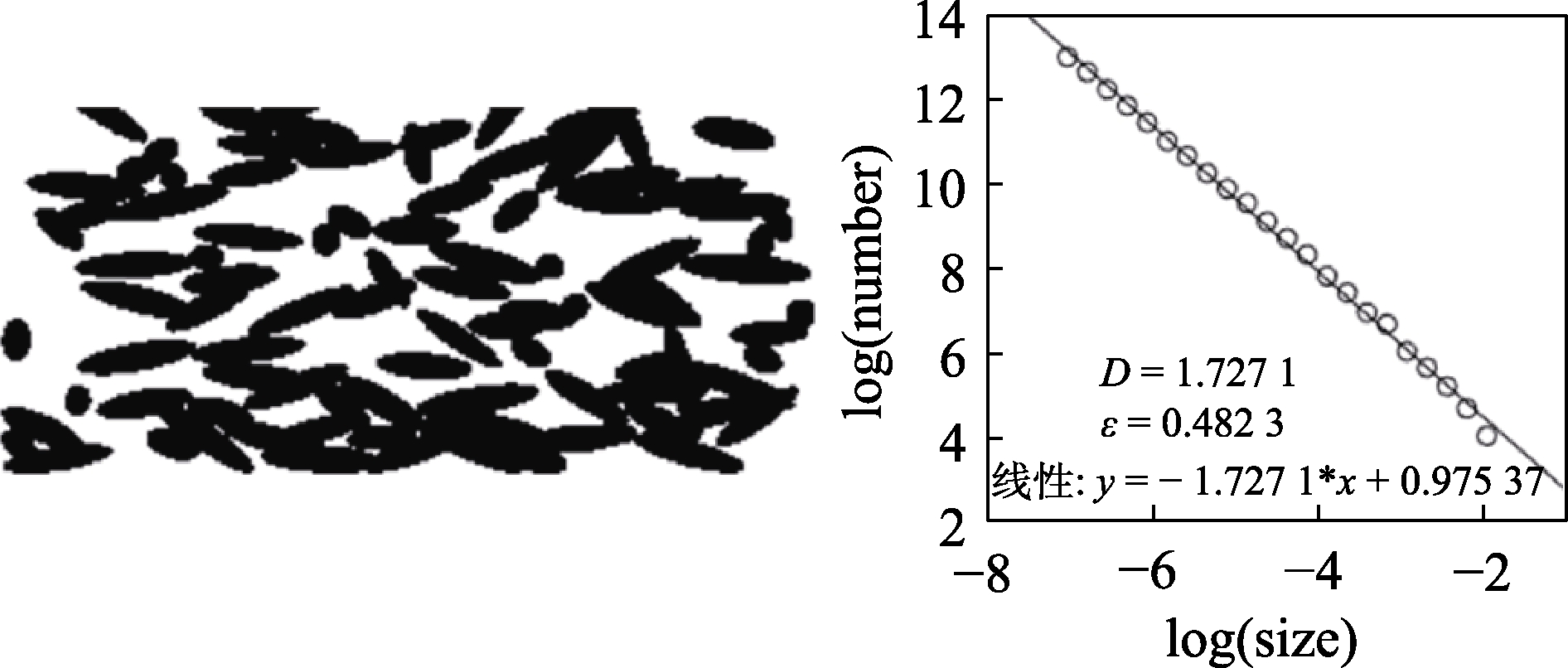
图6 5 000个/s时的分形维数和孔隙率
Fig.6 Fractal dimension and porosity at 5 000/s
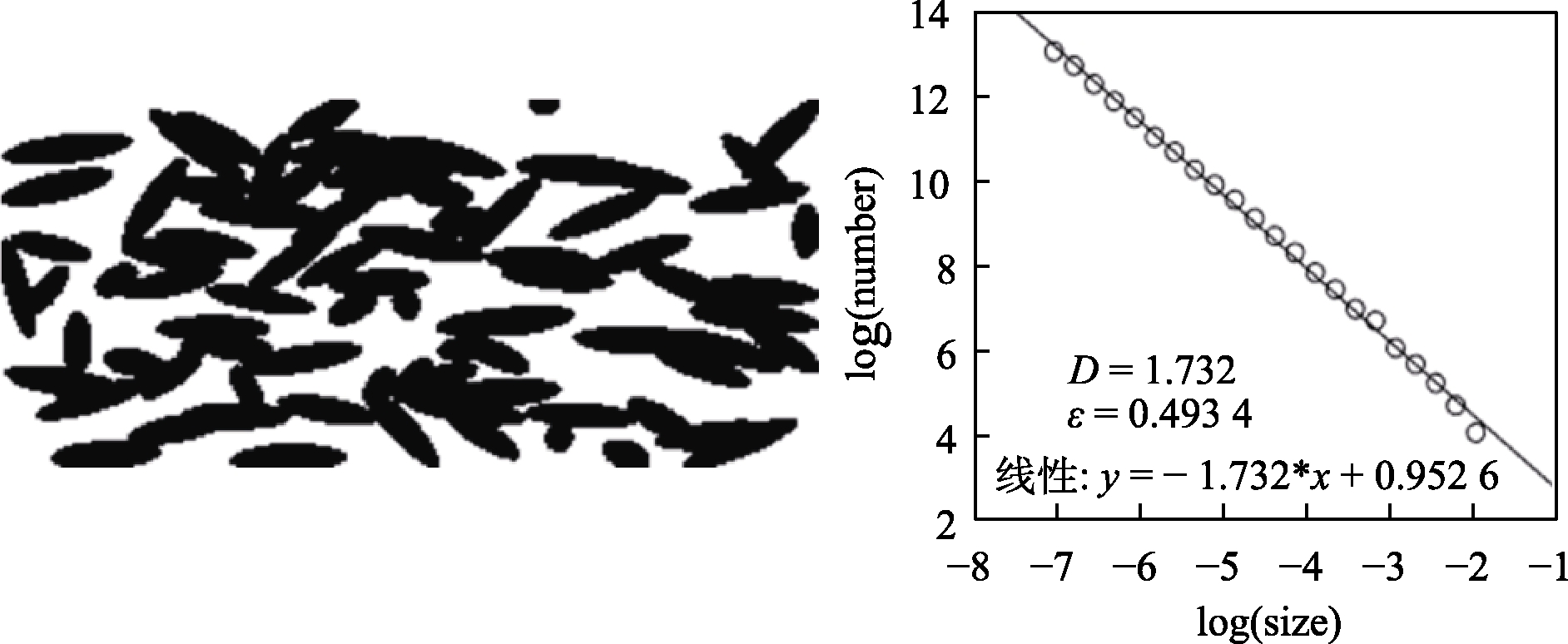
图7 4 000个/s时的分形维数和孔隙率
Fig.7 Fractal dimension and porosity at 4 000/s
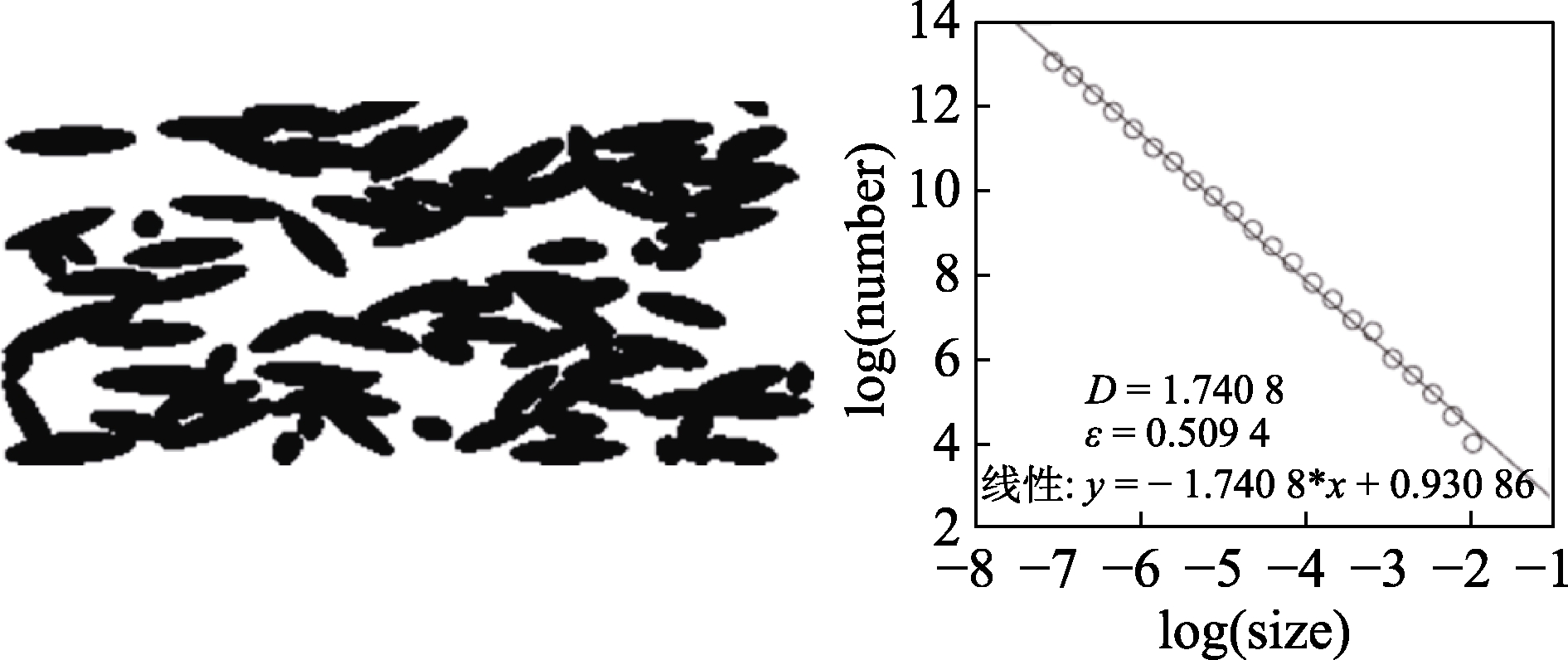
图8 3 000个/s时的分形维数和孔隙率
Fig.8 Fractal dimension and porosity at 3 000/s

图9 2 000个/s时的分形维数和孔隙率
Fig.9 Fractal dimension and porosity at 2 000/s
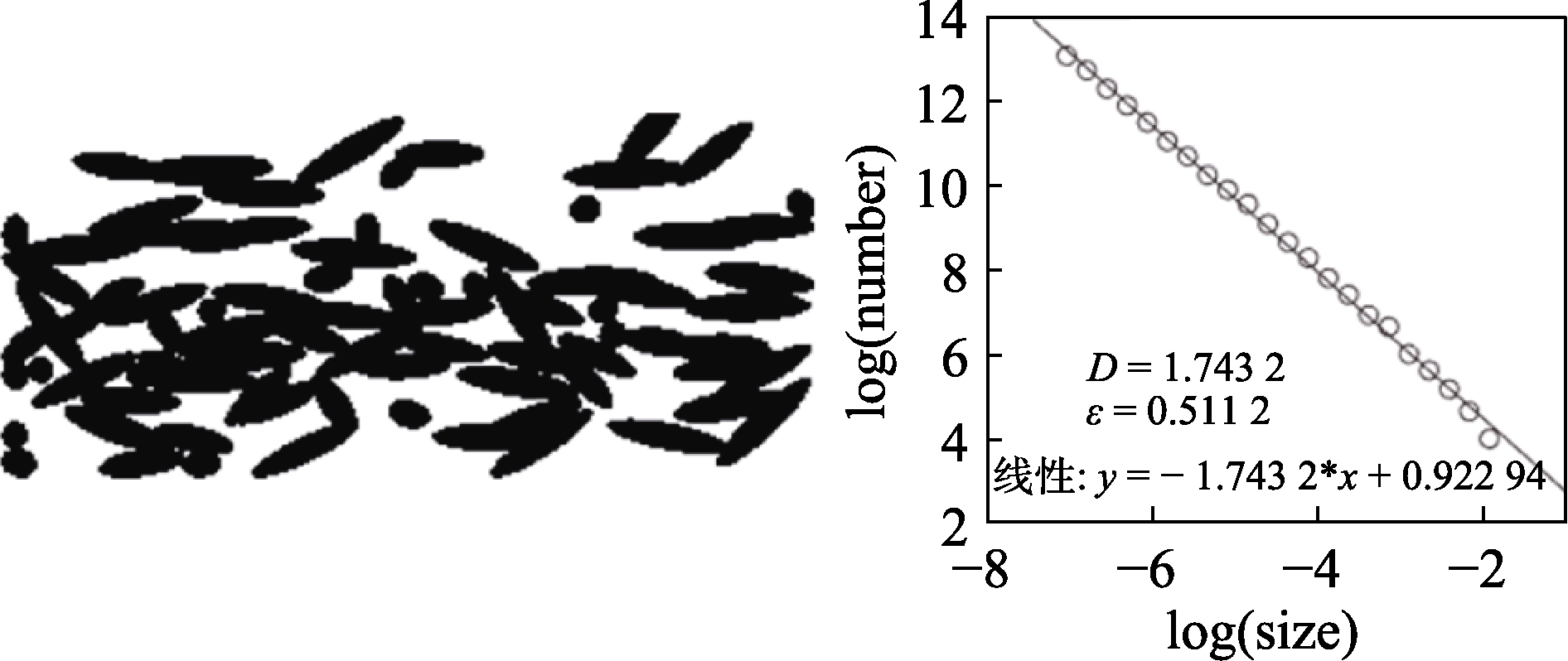
图10 1 000个/s时的分形维数和孔隙率
Fig.10 Fractal dimension and porosity at 1 000/s
此时得到不同入库速度时的分形维数和孔隙率如表2,以便求得对应渗透率。
表2 不同入库速度分形维数和孔隙率
Table 2 Fractal dimension and porosity of different warehousing speeds
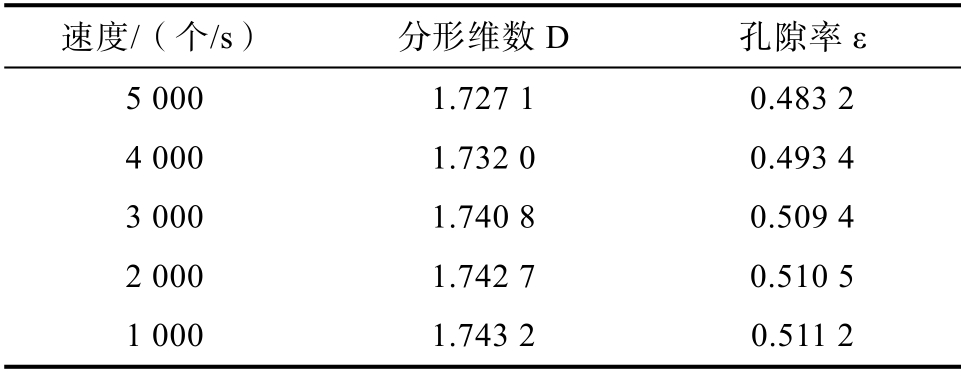
速度/(个/s) 分形维数D 孔隙率ε 5 000 1.727 1 0.483 2 4 000 1.732 0 0.493 4 3 000 1.740 8 0.509 4 2 000 1.742 7 0.510 5 1 000 1.743 2 0.511 2
将表2中的数据带入公式1~3,得到稻谷以不同速度入库时的渗透率,如图11。
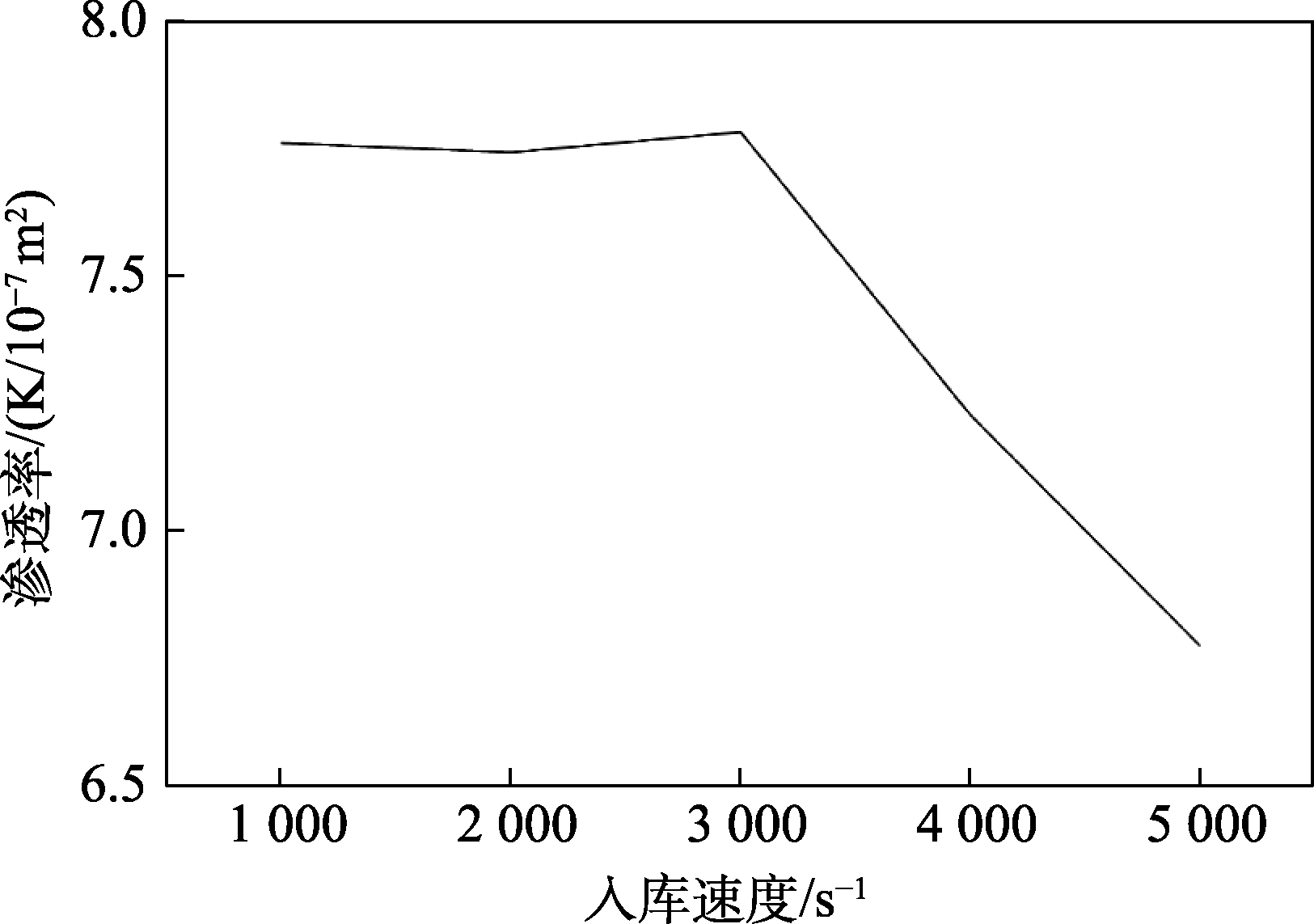
图11 各速度下渗透率的值
Fig.11 Permeability values at various speeds
由图11可以看出,粮堆的渗透率随入库速度的增加有一种下降的趋势,同时速度较低时渗透率差别不大,而速度过慢又会对堆粮工作的效率产生影响,权衡两种因素,得到3 000 个/s是本次模拟中较为合适的入库速度。
由公式5逆推导得到本次模拟较为合理的单个运粮机运粮速度为14.3 t/h,整仓入库速度根据仓房大小选取合适的运粮机个数即可计算求得。
6 粮食的堆积方式对分形维数的影响
由于此次模拟储粮的堆积方式为竖直方向不同的分层分布,沿宽度方向孔隙率和渗透率差别不大,仍然选取稻谷堆宽度方向中间位置截面图来研究。三种情况分别为大小颗粒混合堆积即粮堆自然堆积、大小颗粒分层堆积和大小颗粒分成四层堆积,如下图所示(大颗粒为黑色,小颗粒为灰色),为不同堆积方式的分形维数和孔隙率:
将图12~14中的数据带入公式1~3,得到稻谷以不同堆积方式入库时的渗透率,如图15:
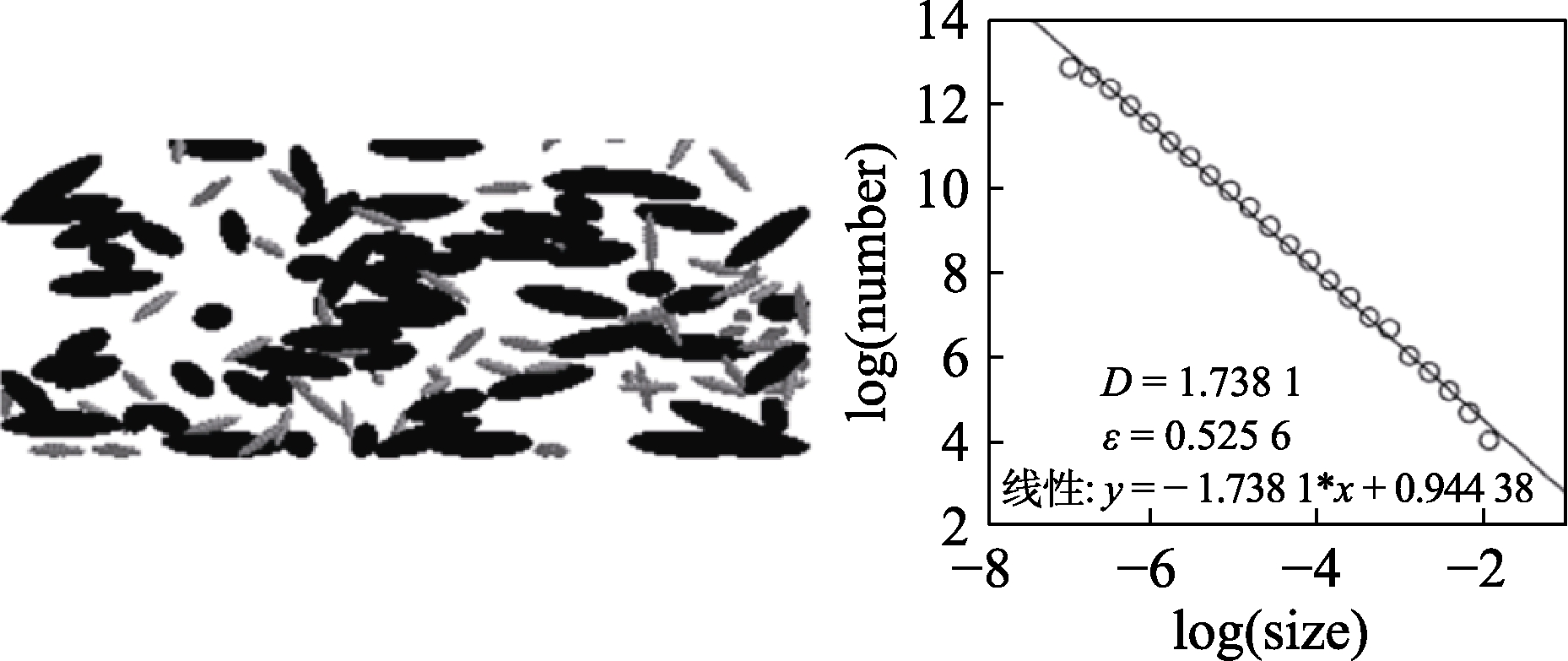
图12 大小颗粒混合时的分形维数和孔隙率
Fig.12 Fractal dimension and porosity of mixed particles

图13 大小颗粒分层时的分形维数和孔隙率
Fig.13 Fractal dimension and porosity of stratified particles

图14 大小颗粒分成四层时的分形维数和孔隙率
Fig.14 F ractal dimension and porosity of large and small particles divided into four layers
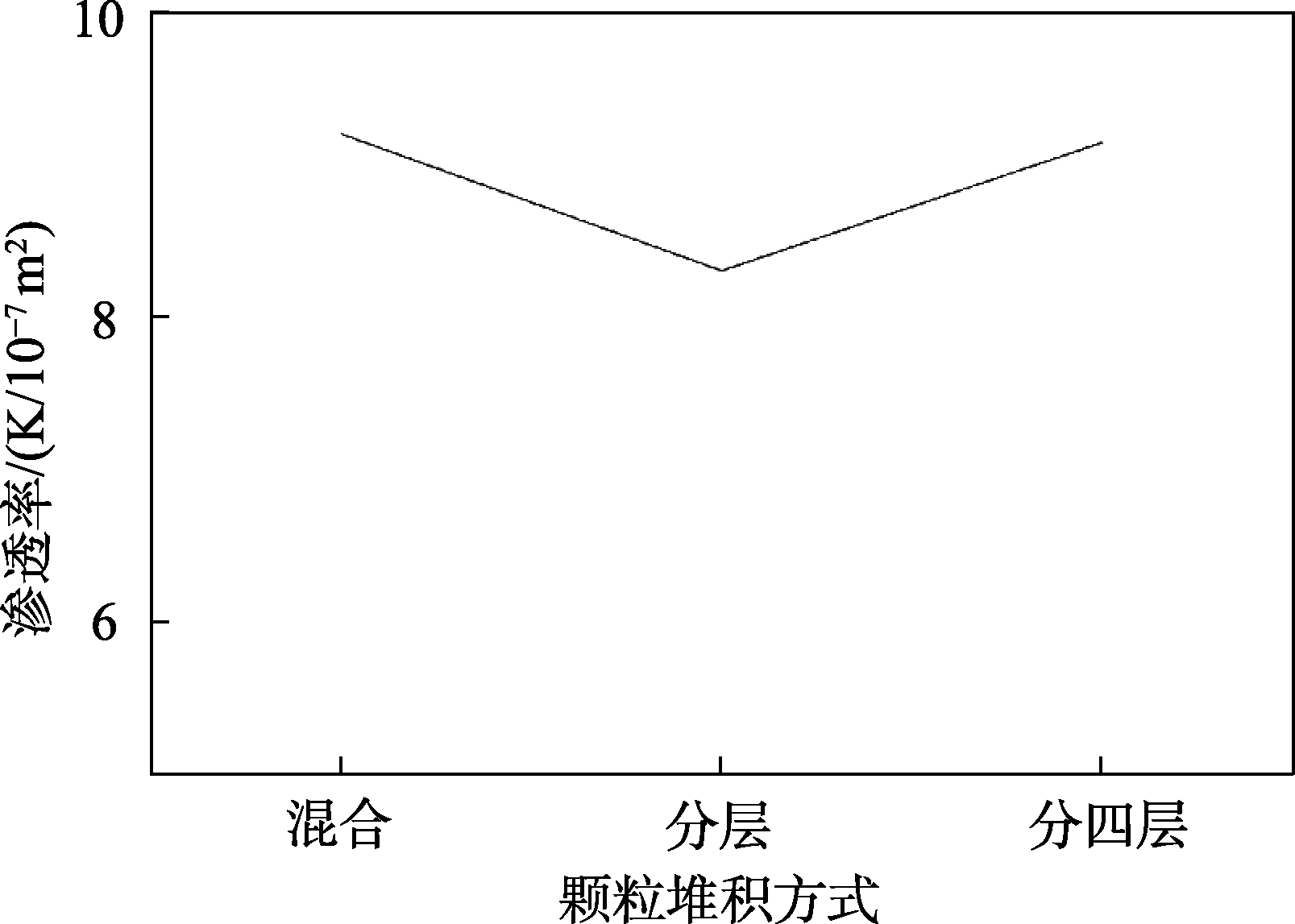
图15 各堆积方式下渗透率的值
Fig.15 Permeability value under each accumulation mode
由图可以看出,由于粮食颗粒较为均匀,模拟的小颗粒较少,三种堆积方式下渗透率差别比较小,同时看出分层越多越接近于混合方式,与实际情况相符。可以看出自然混合方式堆积时粮堆渗透率最大,即自然堆积方式是粮食堆积比较有利的方式。
7 结论
通过以上的模拟与分析,可以得出以下结论:
(1)粮仓堆积的粮堆具有分形特性,可以使用分形理论对多孔粮堆进行研究与分析;
(2)粮堆分形维数与渗透率正相关,较大的粮堆渗透率有利于后续粮堆的温度控制和机械通风降温能耗的降低,即较大的分形维数有利于储粮安全;
(3)堆粮的入库速度对于粮堆的渗透率有较大影响,单个运粮机速度为14.3 t/h时,分形维数较大,渗透率较大,同时不影响堆粮的效率,这对于现实堆粮过程具有参考意义;
(4)粮堆的堆积方式由于粮食本身具有均匀性的特点,所以采用较少的小颗粒进行模拟,发现堆积方式对于渗透率的影响比较少,自由堆积的方式即是对于粮食比较有利的堆积方式。
[1] 雷树业, 王利群, 贾兰庆, 等. 颗粒床孔隙率与渗透率的关系[J]. 清华大学学报(自然科学版), 1998(5): 78-81.LEI S Y, WANG L Q, JIA L Q, et al. Relationship between porosity and permeability of granular bed [J] Journal of Tsinghua University (NATURAL SCIENCE EDITION), 1998(5): 78-81.
[2] JOLL K R, HANRATTY T J. Transition to turbulence for flow through a dumped bed of spheres[J]. Chemical Engineering Science, 1966, 21: 1185-1190.
[3] WEGNER T H, KARABDAS A J, HANRATTY T J. Visual studios of flow in a regular array of spheres[J]. Chemical Engineering Science, 1971, 26: 59-63.
[4] 李瑞川. 多孔介质渗流、干燥特性的分形研究[D]. 昆明理工大学, 2012.LI R C. Fractal study on seepage and drying characteristics of porous media[D]. Kunming University of technology, 2012.
[5] 李福君. 依靠科技创新,建好管好“天下粮仓”[J]. 粮油食品科技, 2013, 21(2): 1-3.LI F J. Relying on scientific and technological innovation, build and manage the “world granary”[J]. Science and Technology of Cereals, Oils and Foods, 2013, 21(2): 1-3.
[6] 桂便, 祝玉华, 甄彤. 卷积神经网络在储粮害虫图像识别中的应用研究[J]. 粮油食品科技, 2018(6): 73-74.GUI B, ZHU Y H, ZHEN T. Application of convolution neural network in image recognition of stored grain pests[J]. Science and Technology of Cereals, Oils and Foods, 2018(6): 73-74.
[7] FALCONER K J. Fractal Geometry, 2nd ed[M]. New York: John Wiley and Sons Press, 2003.
[8] HSU Y L, LAM D K T. Fractal dimension of the surface shape of textile patterns[C]. IEEE, 2010.
[9] 梁东方,李玉梁,江春波. 测量分维的数盒子算法研究[J]. 中国图像图形学报, 2002, 3(7): 246-250.LIANG D F, LI Y L, JIANG C B. Research on number box algorithm for measuring fractal dimension[J]. Chinese Journal of image and graphics, 2002, 3(7): 246-250.
[10] 郑佳宜, 戴晓丽, 陈振乾. 多孔介质孔隙结构重构及水蒸气传递特性[J]. 土木建筑与环境工程, 2014, 5(36): 45-49.ZHENG J Y, DAI X L, CHEN Z Q. Pore structure reconstruction and water vapor transfer characteristics of porous media[J]. Civil architecture and environmental engineering, 2014, 5(36): 45-49.[
11] 刘耀民, 刘中良, 黄玲艳. 计盒维数的算法优化及其在结霜现象中的应用[J]. 北京工业大学学报, 2012, 38(11): 1724-1730.LIU Y M, LIU Z L, HUANG L Y. Optimization of box counting dimension algorithm and its application in frost phenomenon[J].Journal of Beijing University of technology, 2012, 38(11): 1724-1730.