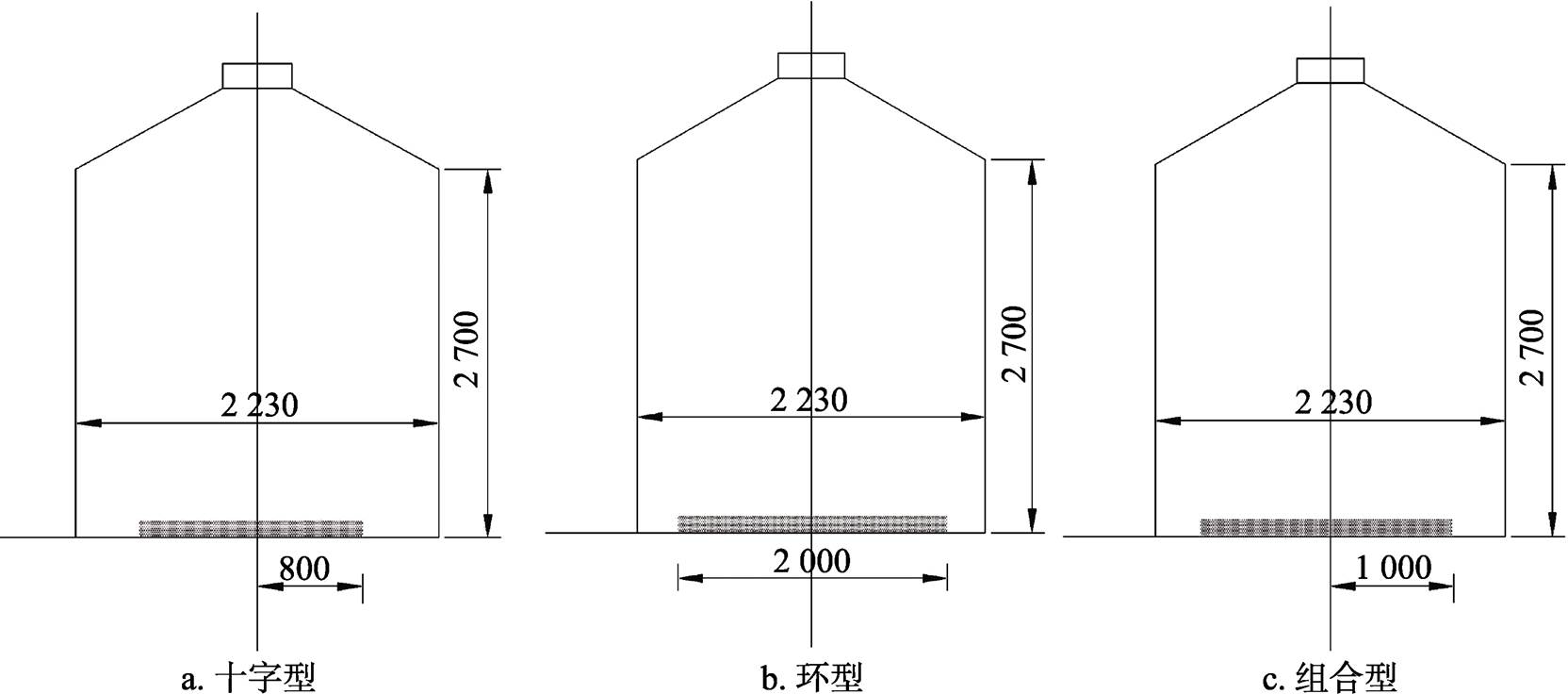
图1 三种浅圆仓剖面图/mm
摘 要:基于多孔介质流动和热湿耦合传递理论,推导得到了浅圆仓的粮堆内部动量方程、能量方程和水分守恒方程,通过数值求解法解决仓储粮堆的自然对流、热量传递和水分传递之间的问题。采用Fortran编程的方法,针对浅圆仓的十字型通风道、环型通风道、组合型(十字型加环型)通风道的通风效果进行了数值模拟分析。结果表明:组合型通风道相比其它两种通风道仓内气流分布更加均匀,降温保水效果最好,更有利于粮食的安全储存和节能降耗。为浅圆仓通风道的选择和设计提供了理论指导和依据。
关键词:浅圆仓;通风道;热湿传递;数值模拟;通风效果
粮食的数量和质量安全是维持人们生活重要保障。粮食自收获后产生的损失总量大约为10%~30%,其中主要损失是在储存过程。为减少粮食储藏过程的损失,主要考虑温度和水分含量的影响,将粮堆内部温度维持在低于15℃,水分含量在12%~12.5%内,可以最大程度保持粮食颗粒的活性,抑制害虫及微生物的滋生。对粮仓进行通风,将粮食的温度和水分含量控制在合理范围内,就可以保证粮食的安全储存。
使用数值模拟方法求解粮堆模型的传热传质问题是近年来发展的一种基于计算机程序的新方法[1],是一种可合理设计粮仓通风方案的数值分析工具。近年来,科研人员在原有数值模型的基础上,完善了包含热量与水分转移的相互作用的模型[2]。Thompson开发了一个实验和数值模拟相结合的数值模拟模型,通过连续的环境通风来评估温湿度对粮食储存的影响[3]。Thorpe通过概述不同通风方式对粮堆内部气流速度和干物质损耗的影响,提出通风过程中有关粮食颗粒内部的热湿传递的有限差分数学模型[4]。上述模型的局限性在于只考虑粮堆内部的温湿度变化,忽略了仓外太阳辐射区与粮仓顶部空气区域和储粮区域之间的热湿耦合过程。王远成等人[5]对双区域模型中温度和水分含量进行了系统的量化分析与验证。
基于多孔介质热湿耦合传递理论和局部热平衡原理,建立了一个模拟平底浅圆仓流动和热湿传递的通风数值模型。针对现有的计算流体力学模拟程序存在耗费时间长,且对电脑硬件设备要求较高的弊端[6]。利用Frotran语言编写运行程序, 对通风过程中浅圆仓内部的小麦水分场和温度场变化进行了模拟,并将所得模拟数据与实验数据作对比,从而验证该程序的准确性[7]。同时,针对三种不同型式的通风道,对浅圆仓内的通风效果进行模拟研究。
选取了一个高度为2.7 m,直径为2.23 m的平底浅圆仓作为研究对象,其剖面图、俯视图分别如图1、图2所示。三种通风道型式分别为十字型、环型和组合型(浅圆仓通风道常见形式是梳型、放射型和多环形)。本文主要研究以放射型为基础出发的十字型、环型和组合型三种不同通风道位置对通风效果的影响,如图1a、图1b、图1c和图2a、图2b、图2c所示。

图1 三种浅圆仓剖面图/mm
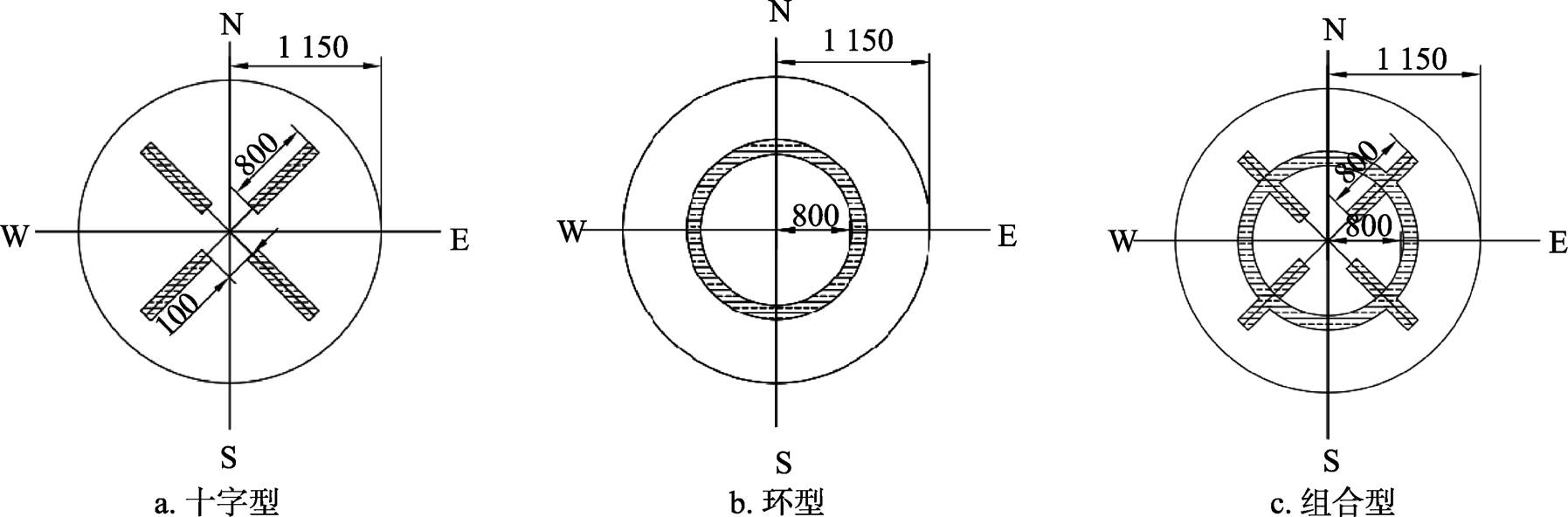
图2 三种浅圆仓俯视图/mm
基于局部热平衡原理和多孔介质流动传热传质理论,考虑到粮堆内部的热湿耦合和太阳辐射的影响,建立储粮机械通风过程中粮堆内部的热湿传递和流动的数学模型。
通过对直角坐标的转换,用柱坐标(r,φ,z)表示浅圆仓的粮堆内部动量方程、能量方程和水分守恒方程以及包含边界条件的控制方程的模 型[8]。其中,r为半径方向,φ为角度方向,z为高度方向。
1.2.1 动量方程
在变换之后的柱坐标下,当时间趋近于无穷时,粮堆内部压力场的控制方程符合拉普拉斯公式,可表示为:
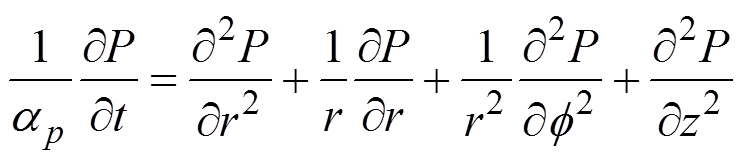 (1)
(1)式中:P为粮堆的压力,Pa;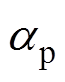 是一个假设的瞬变因子,Pa。
是一个假设的瞬变因子,Pa。
柱坐标下半径、圆周和垂直方向的速度分量分别可由式(2)、式(3)、式(4)表示:
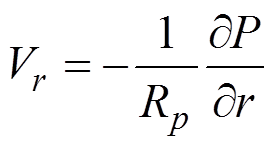 (2)
(2)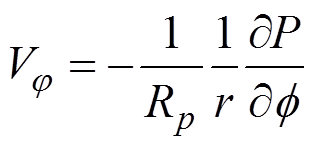 (3)
(3)
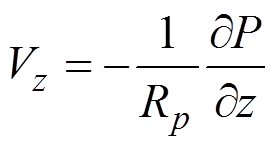 (4)
(4)
式中:Rp为空气有效阻力系数,Pa·s/m。
1.2.2 能量守恒方程
根据局部热平衡理论,热平衡公式可以由式(5)表示:
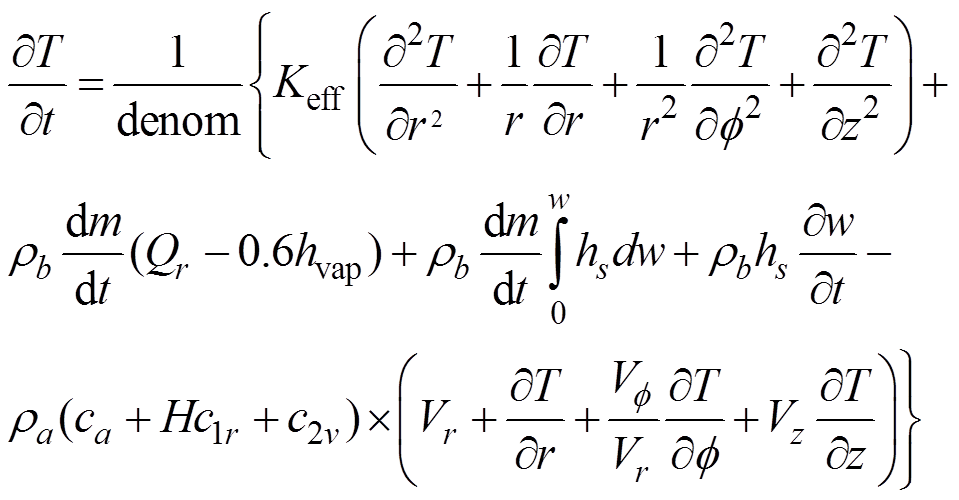 (5)
(5)式中:
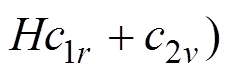 ;T和W分别为粮堆内部的温度和水分含量,单位分别为K和kg;H为空气中的绝对湿度,kg/kg;
;T和W分别为粮堆内部的温度和水分含量,单位分别为K和kg;H为空气中的绝对湿度,kg/kg;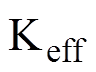 为有效热扩散量,
为有效热扩散量,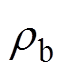 为粮堆的密度,
为粮堆的密度,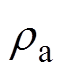 为干空气的密度,
为干空气的密度,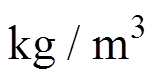 ;
;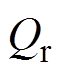 为粮堆累计消耗量,
为粮堆累计消耗量,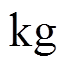 ;
;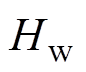 、
、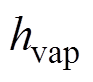 、
、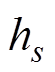 分别为粮堆放出、自由水放出和粮堆吸收的热量,
分别为粮堆放出、自由水放出和粮堆吸收的热量,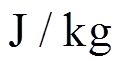 ;
;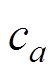 、
、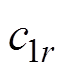 、
、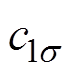 、
、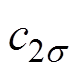 分别为干空气、水蒸气、液态水、粮食的比热容;
分别为干空气、水蒸气、液态水、粮食的比热容;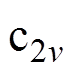 为潜热方程的特定常数,J/kg/K;
为潜热方程的特定常数,J/kg/K;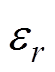 为粮堆的孔隙率;
为粮堆的孔隙率;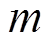 为干物质质量,kg;
为干物质质量,kg;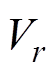 、
、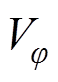 、
、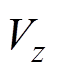 分别为半径、角度和高度方向上的分速度,
分别为半径、角度和高度方向上的分速度,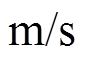 。
。
1.2.3 水分守恒方程
水分守恒方程可由式(6)表示:
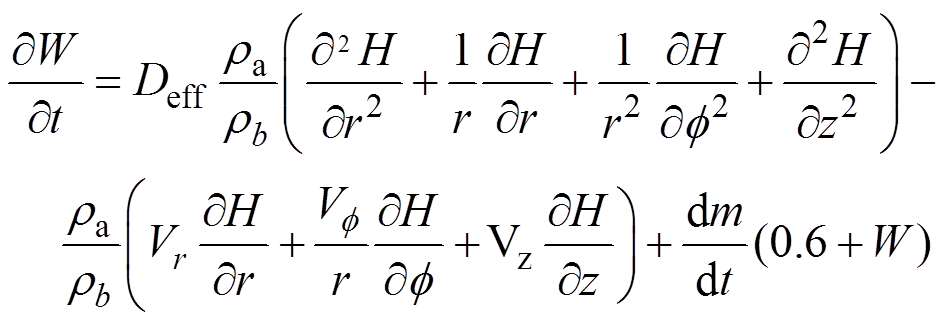 (6)
(6)式中: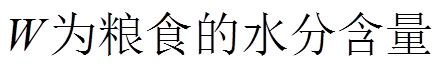 ,%;
,%;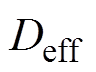 是由Thorpe提出来的表示有效扩散率,
是由Thorpe提出来的表示有效扩散率,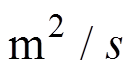 ;
; ;
;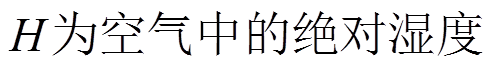 ,
,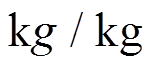 ;
;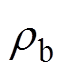 、
、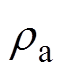 分别为粮堆的密度和干空气的密度,
分别为粮堆的密度和干空气的密度,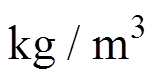 。
。
模拟的粮食品种为小麦,其孔隙率为0.44,比热容为cp=1 790 J/kg×K,粮堆的初始温度和初始水分含量分别为30 ℃和15%。进口空气的温度和水分含量分别为23 ℃和 15%,吨粮通风量为5.6 m3/h×t,借助编程实现粮堆内部的通风模拟。
图3所示为速度场分布情况,图3a图3b图中黑色区域表明速度很小,为e-02个数量级,图3c中由黑色、灰色到浅灰色区域气流速度依次减小,但都保持在e-03个数量级。由此可得出结论:十字型通风系统和环型通风系统提供的粮仓内部气流分布不均匀,集中在通风道附近的速度梯度大;组合型通风系统在通风60 d后仓内的速度分布较为均匀,速度数据相对于浅圆仓中心轴大致呈对称分布,由此可知组合型通风道的通风性能更好,有利于粮堆内部的热湿传递[9]。
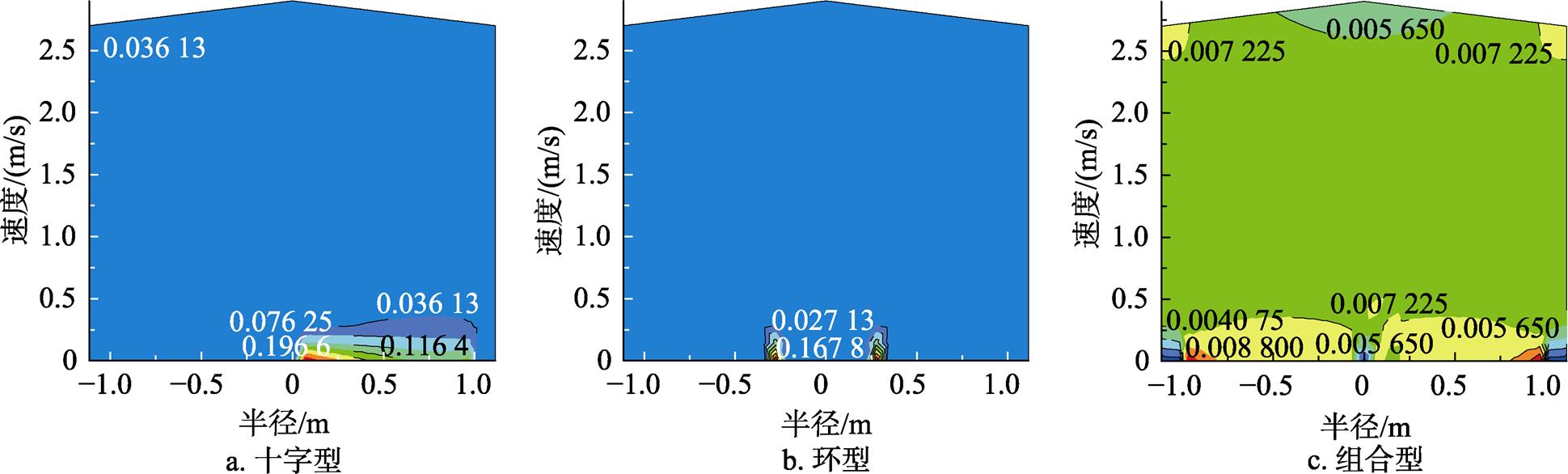
图3 三种通风形式下粮堆内部的速度分布图
为进一步表征不同通风系统的速度均匀性,对于不同通风道通风效果进行评价,可以采用均匀性指数来评价浅圆仓内气流流速分布的均匀程度[10]。采用Weltens等建立的评价流动分布特性的均匀性指数来表示流速混合的均匀性程度,用式(10)表示。
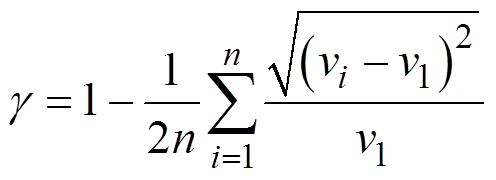 (10)
(10)式中: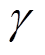 为均匀性指数,在0和1之间变化;
为均匀性指数,在0和1之间变化;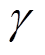 越大说明流场分布越均匀;
越大说明流场分布越均匀;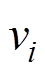 为各测点的速度;
为各测点的速度;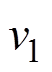 为全部节点的平均速度;n为模拟节点数。
为全部节点的平均速度;n为模拟节点数。
利用公式(10)整理模拟结果的相关数据,计算通风结束时(60 d)(通风的吨粮通风量为5.6 m3/h×t,为实现降温保水效果通风60 d,若在60 d之前降到目标温度,可适当减少通风天数。吨粮通风量的经验参数一般在2~5.5 m3/h×t之间取值)纵截面上气流分布的均匀性指数如表1所示。
表1 三种通风系统的速度分布
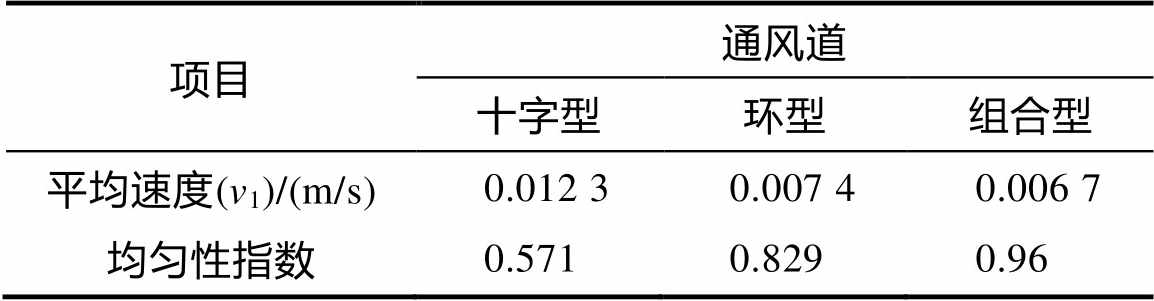
项目通风道 十字型环型组合型 平均速度(v1)/(m/s)0.012 30.007 40.006 7 均匀性指数0.5710.8290.96
由表1数据可以看出: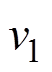 值为本程序模拟出的882个节点的平均速度值,半径方向、角度方向和高度方向的分布个数分别为21×2×21个,各测点速度取程序输出的表观速度,即粮堆颗粒表面的风速大小。将平均速度数据代入式(10),可以计算出三种通风系统的均匀性指数。由表1可知环型通风系统的粮堆内部气流均匀程度高于十字型通风系统,是因为环型通风道占据的空间位置均匀;组合式通风系统的粮仓内部均匀性指数为0.96,其数值最接近于1,证明该通风形式下气流流速更均匀分布于粮仓内部。
值为本程序模拟出的882个节点的平均速度值,半径方向、角度方向和高度方向的分布个数分别为21×2×21个,各测点速度取程序输出的表观速度,即粮堆颗粒表面的风速大小。将平均速度数据代入式(10),可以计算出三种通风系统的均匀性指数。由表1可知环型通风系统的粮堆内部气流均匀程度高于十字型通风系统,是因为环型通风道占据的空间位置均匀;组合式通风系统的粮仓内部均匀性指数为0.96,其数值最接近于1,证明该通风形式下气流流速更均匀分布于粮仓内部。
参照计算速度均匀性指数的公式,结合输出各节点的平均温度,可得出纵截面上的温度均匀性指数如表2所示。
表2 三种通风系统的温度分布
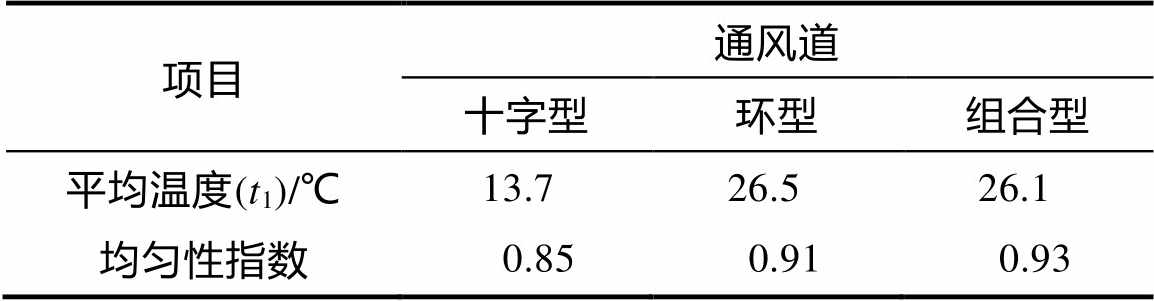
项目通风道 十字型环型组合型 平均温度(t1)/℃13.726.526.1 均匀性指数0.850.910.93
对比表2给出的数据可以看出:三种通风系统下的温度均匀性指数相差不大,环型通风系统的温度均匀性能仍优于十字型通风系统[11]。组合型通风系统的均匀性指数最接近于1,证明组合型风道进行通风的时候,粮仓内部的温度分布更为均匀,有利于通风过程中仓储粮堆达到降温的效果。
对于浅圆仓内的通风研究,需要同时考虑热传导和热对流对粮仓内部热湿传递的作用。模拟程序中的三种通风系统均设置为相同的初始条件,唯一区别在于底部的通风道位置不同。通过程序输出粮堆内部温度和水分含量数据,将所得数据导入后处理软件得到平底仓内部温湿度场的分布图形。
引起仓内储粮温度发生变化的热源分为内部热源和外部热源。外部热源主要指仓体外部的大气环境,不可忽略的是太阳辐射对仓储粮堆内部温度的影响,它会作用于仓顶和壁面并在此处产生热量迁移,从而改变粮仓内部的热环境[12]。十字型通风道、环型通风道和组合型通风道浅圆仓内纵截面上温度分布如图4所示,圆截面上温度分布如图5所示。
从图4可以看出靠近通风道处的温度下降最快,每种通风系统中两侧的壁温不完全对称,这是由于东、南、西、北四个区域的墙体温度受太阳辐射不同而造成的[13]。由于风道在粮仓内的布置是对称的,可以从图5中明显看出温度场的分布近似为对称分布。
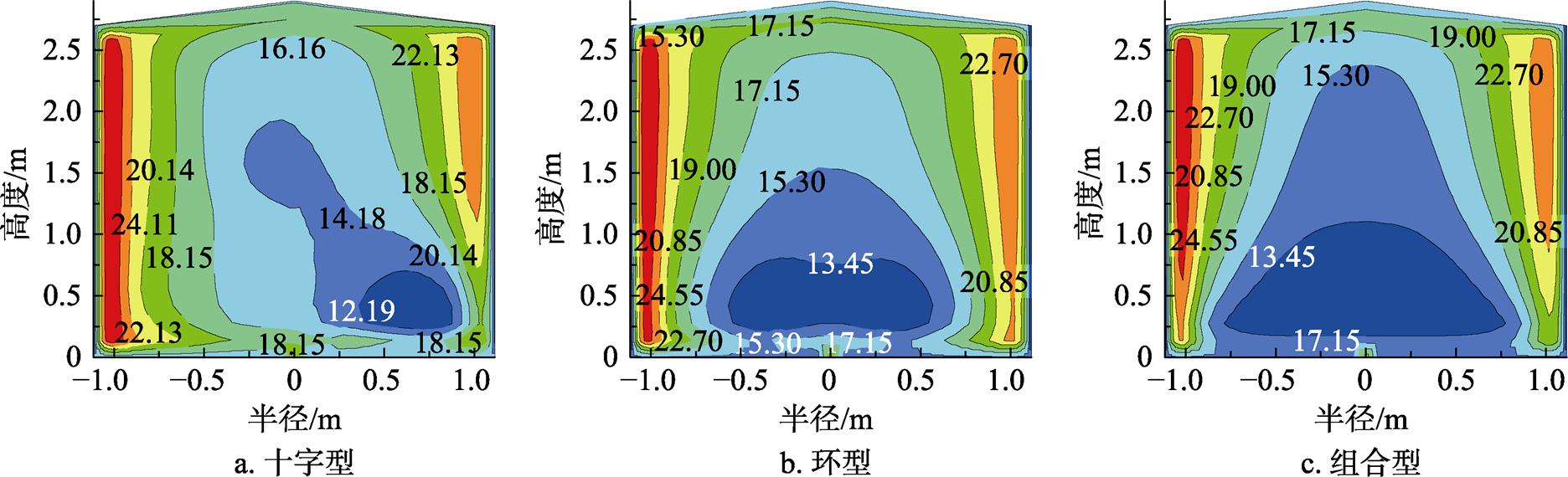
图4 三种通风形式的纵截面温度分布图
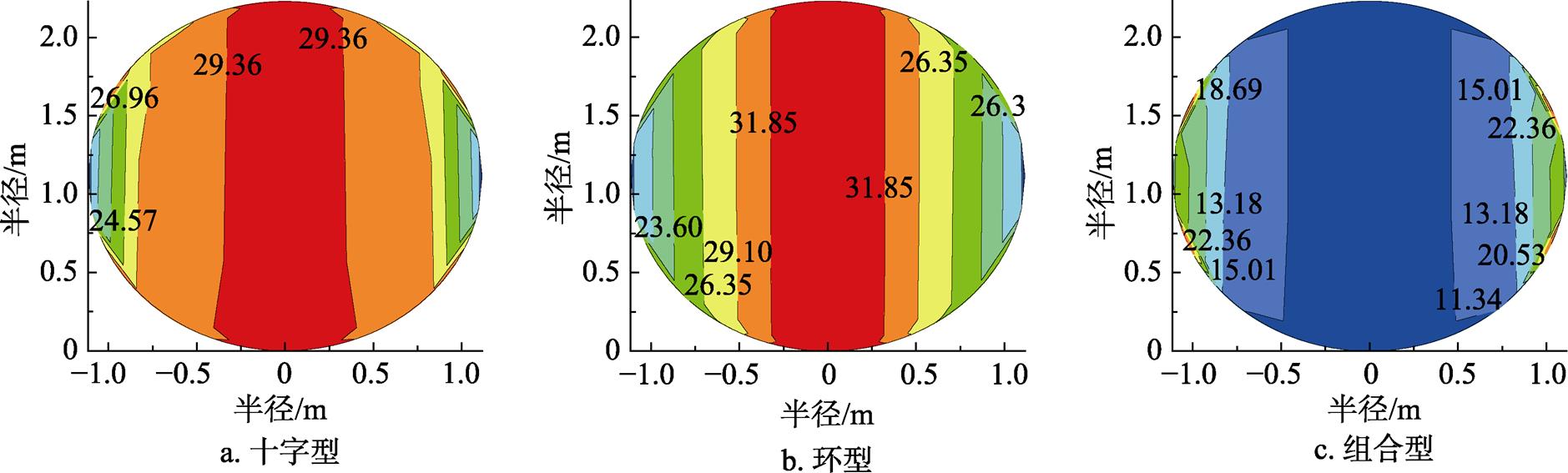
图5 温度在圆截面上的分布图(中间高度)
浅圆仓内粮食初始温度皆为30 ℃,结束60 d的通风之后,平均温度数据如表3中所列。可以得出结论:组合型通风系统通风结束时的温度值降到最低,单位时间(1 d)内的平均温度变化速率值为三种通风系统中的最大值,达到0.27 ℃/d,组合型通风系统降温快的优势在此体现。
程序模拟为期60 d的通风后,得出图6和图7所示的十字型通风道仓、环型通风道仓、组合型通风道仓内的纵截面、圆截面上的水分分布图。
表3 模拟的平均温度变化速率的对比
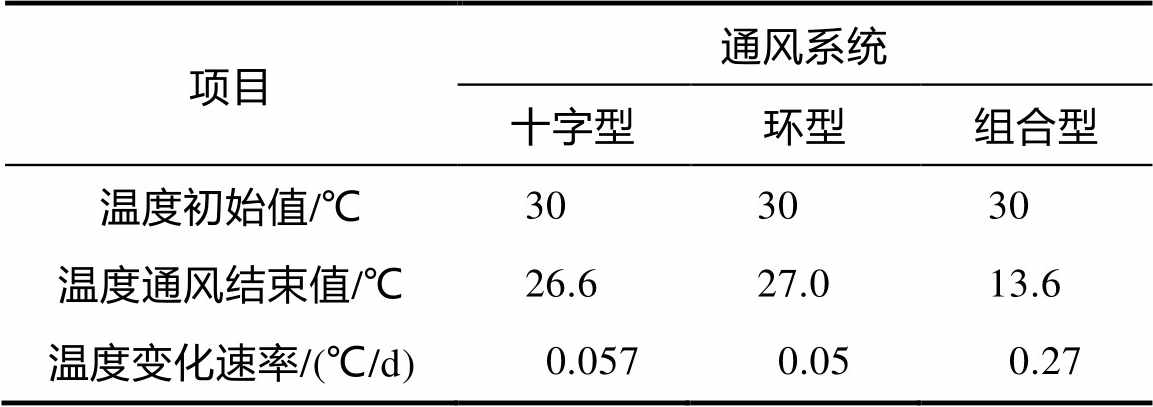
项目通风系统 十字型环型组合型 温度初始值/℃303030 温度通风结束值/℃26.627.013.6 温度变化速率/(℃/d)0.0570.050.27
由图6和图7可以看出在浅圆仓通风的初始阶段,由于通风机工作引起附近粮食湿度高、温度低,随着通风时间的增加,通风道附近的水分含量高于浅圆仓其他区域的水分含量[14]。对比图6和图7所示的通风结束时的水分场分布,可知组合型通风系统在通风结束时的水分含量变化最小,这是因为组合型通风道比其它两种通风道的面积大,使得粮食通风效果更好。
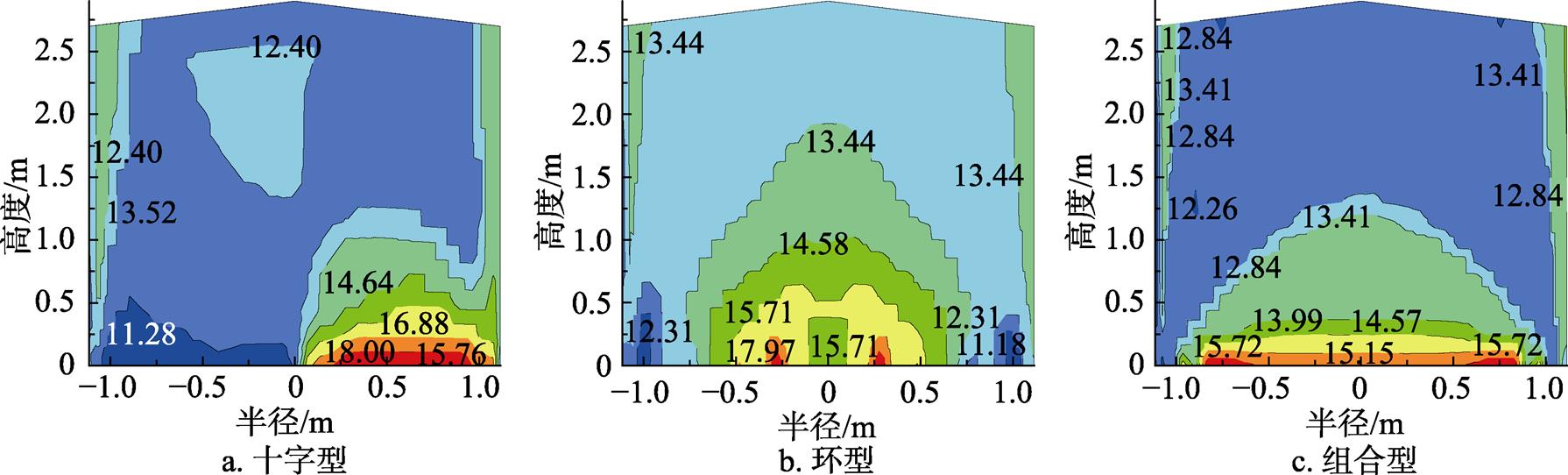
图6 三种通风形式的纵截面水分分布图

图7 水分在圆截面上的分布图(中间高度)
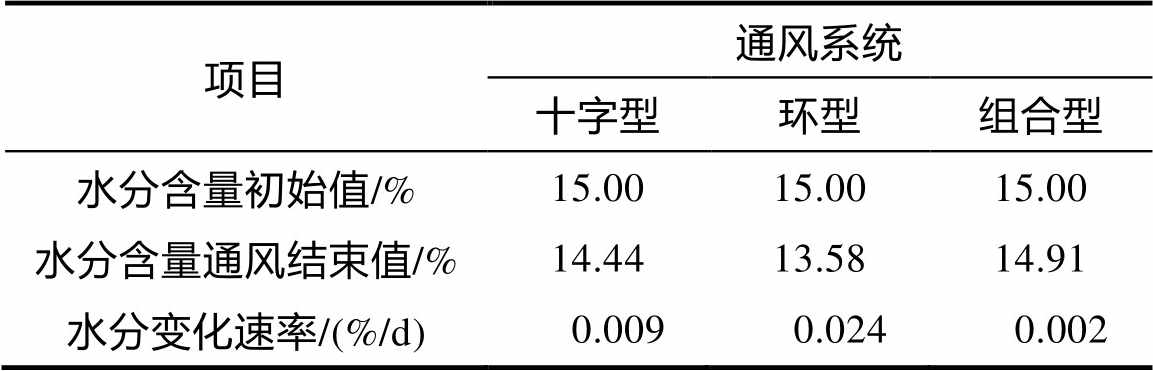
由表4可以看出:十字型、环型和组合型通风道三种形式下,粮堆的水分含量初始值都为15.00%,经过60 d的通风后,在通风结束时粮堆内部的水分含量皆有下降。环型通风系统的水分变化速率达到0.024%/d,水分含量损失明显,而组合型通风系统中水分变化速率为0.002%/d,机械通风后粮食的保水性能最好。
表4 模拟的粮堆平均水分变化速率对比
项目通风系统 十字型环型组合型 水分含量初始值/%15.0015.0015.00 水分含量通风结束值/%14.4413.5814.91 水分变化速率/(%/d)0.0090.0240.002
设置三种不同通风道形式,对比每种通风形式通风结束时的温度和速度数据,发现选用组合型通风道进行通风时,浅圆仓内部气流均匀性指数更高,表明组合型通风形式下的气流更为均匀地分布于仓储粮堆内部。
十字型通风道提供的气流分布不均匀,造成粮仓内部部分区域得不到送风,降温效果无法实现,高温会使粮堆产生霉变和虫害,不利于粮食的安全储存。但是当某些特殊位置需要降低到特定温度时,可以利用气流分布不均匀这一特点在粮堆内部实现局部区域的降温干燥效果。
由于环型通风道在圆周方向是连续通风道,其气流均匀性能优于十字型通风道,但弊端在于径向方向气流流动较慢,此方向上的热湿传递过程缓慢。
相较于其它两种通风形式,组合型通风系统的平均温度变化速率高、平均水分变化速率低,粮仓内部温度降低快且水分损失量小,证明组合型通风系统降温保水的性能最佳。
参考文献:
[1] 王远成, 张忠杰, 吴子丹, 等. 计算流体力学技术在粮食储藏中的应用[J]. 中国粮油学报, 2012, 27(5): 86-91.
[2] 陈桂香, 岳龙飞, 王振清, 等. 钢筋混凝土地下粮仓准静态温度场数值模拟[J]. 中国粮油学报, 2014, 29(3): 79-83.
[3] THOMPSON T L. Temporary storage of high-moisture shelled corn using continuous aeration[J]. Transaction of American Society of Agriculture Engineers. 1972, 15(2): 333-337.
[4] THORPE G R. The application of computational fluid dynamics codes to simulate heat and moisture transfer in stored grains[J]. J Stored Prod Res, 2008, 44(1): 21-31.
[5] 王远成, 潘钰, 尉尧方, 等. 仓储粮堆内部自然对流和热湿传递的数学分析和验证[J]. 中国粮油学报, 2017, 32(9): 120-130.
[6] 吴子丹, 赵会义, 曹阳, 等. 粮食储藏生态系统的仿真技术应用研究进展[J]. 粮油食品科技, 2014, 22(1): 1-6.
[7] 李岩峰, 张来林, 曹阳, 等. 小麦导热系数的测定[J]. 河南工业大学学报(自然科学版). 2010(1): 68-70.
[8] CONVERSE H H, GRACES A H, CHUNG D S. Transient heat transfer within wheat stored in a cylindrical bin[J]. Transaction of American Society Agriculture Engineering, 1973, 16(1): 129-133.
[9] JIEHEI ZHANG, AJAYKUMAR GUPTA, JOHN BAKER. Effect of relative humidity on the prediction of natural convection heat transfer coefficients[J]. Heat Transfer Engineering, 2007, 28(4): 94-102.
[10] 潘钰, 王远成, 邱化禹, 等. 粮仓机械通风阻力和均匀性模拟研究[J]. 山东建筑大学学报, 2016, 31(3): 255-258.
[11] 邱化禹, 王远成, 高帅, 等. 横向通风系统充氮气调的数值模拟与现场试验对比[J]. 粮食储藏, 2015, 44(6): 22-26.
[12] Fahad G Al-Amri, Maged A I El-Shaarawi. Combined forced convection and surface radiation between two parallel plates[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2010, 20(2): 22-26.
[13] 张辰, 朱君生. CFD仿真技术在粮食仓储上的应用[J]. 粮油仓储科技通讯, 2018, 34(4): 18-19.
[14] 张达, 郑德乾, 陈桂香, 等. 高大平房仓散装粮堆压力场FLAC~(3D)数值模拟[J]. 河南工业大学学报(自然科学版), 2017, 38(6): 98-103. 
Simulation study on ventilation effect of three different ventilation ducts in squat silos
Abstract: Based on the theory of flows through porous media and coupled heat and moisture transfer, the momentum equation, energy equation and water conservation equation for interior of grain pile in squat silo were derived. The problems such as natural convection, heat transfer and moisture transfer of stored grain were solved by numerical solution. The ventilation effect of cross ventilation duct, annular ventilation duct and combined (cross and annular type) ventilation duct of squat silo was analyzed by numerical simulation with Fortran language. The results show that air distribution in combined (cross and annular type) ventilation duct are more evenly than that in the other two types of air ducts, which has the best effect of cooling and water conservation, therefore more propitious to the safe storage and energy saving. The result can provide theoretical guidance and basis for the selection and design of ventilation duct for squat silos.
Key words:squat silo; ventilation duct; heat and moisture transfer; numerical simulation; ventilation effect
DOI: 10.16210/j.cnki.1007-7561.2019.02.012
中图分类号:TS210.1;S379.5
文献标识码:A
文章编号:1007-7561(2019)02-0061-06
收稿日期:2018-08-15
基金项目: 国家重点专项(2016YFD0400100, 2016YFD0401002),国家粮食公益专项(201513001)