张 成,樊洪明
(北京工业大学,北京 100124)
摘 要:对平房仓粮食通风中空气流速分布问题进行CFD数值模拟。考虑粮仓压力的分布,针对通风笼式通风中所采用的通风笼进行独立建模分析,获得其阻力和风速关系数据。并将其应用于粮仓整体数值模型中,提升了模拟的真实性。基于某粮库所采用的粮堆“插管”技术进行粮堆插管模拟,并对插管效果进行评估。结果表明:通过粮堆插管的合理布置,可使粮食内部空气流动速度得到有效改善。通过对插管附近流场、压力场的观察,给出了插管提升通风效果的原理和插管优化设计的方向。
关键词:粮食通风;空气流速 CFD;通风笼;插管
粮食储藏问题直接关系到中国粮食安全和世界粮食安全。粮堆通风对于降低和均衡粮温,调节粮食水分,防止粮堆结露或水分转移具有重要意义,粮食通风技术水平直接影响着粮食仓储质量。
搭建实验粮仓、对粮堆布置测点以检验各种通风方式效果,直接获取粮食内部各种参数,如风速、压力、温度、空气相对湿度等,为粮食仓储安全提供重要经验和数据支持。近年来随着计算机容量的提升和计算技术的进步,计算流体动力学(CFD)作为一种新的研究手段被引入粮食仓储领域,许多学者对粮仓中空气流动进行CFD模拟,该方法可以更快、更全面地对各方案粮仓通风效果进行验证。粮仓内数值仿真研究目前已涉及仓内空气流动以及传热和传质。CFD技术将连续的物理量离散到存储数据的节点上,通过求解流体力学中的连续性方程、动量方程,并结合实验得到的湍流模型,得到仓储维护结构以及粮堆内部的速度场、压力场、温度场等信息。
在粮食储藏数值仿真方面,张忠杰等使用CFD方法研究了准静态仓储粮堆的温度场随季节变化状况[1]。Wang等基于CFD技术对就仓降温冷却和干燥通风时粮堆内部温度和水分的变化过程进行了数值模拟研究,并与试验结果进行了比较[2]。任广跃等采用商业软件Fluent对浅圆钢板仓机械通风时的粮仓内部压力进行了模拟,并与实验粮仓进行了对比[3]。彭威对粮仓内压力、速度、温度进行模拟,且考虑了室内小型钢板方仓、室外浅圆仓、大型平房仓等各种类型粮仓[4]。河南工业大学陈桂香等建立了含有“U”型通风笼沟的粮仓CFD模型[5-6],张海红建立的模型中,也考虑了“丰”字形地上通风笼[7]。但目前的CFD仿真工作中,张海红建立的模型中,也考虑了“丰”字形地上通风笼[7]。但目前的CFD仿真工作中,几乎没有考虑通风笼孔板本身的模型。地上通风笼孔板具有一定的开孔率,通风时存在空气阻力。因此通风数值仿真的可靠性与通风笼孔板模型密切相关。本文拟对通风笼孔板阻力特性进行相关模拟研究,根据实验测定孔板边界条件参数的方法测定孔板周围空气的流速和通过孔板的压降,并通过测试数据推算出压力阶跃孔板通风笼的渗透性和压力阶跃系数,根据推算的参数设置孔板通风笼加入到实际模型中,对比了模型中是否加入孔板边界条件对通风笼内压力值的影响。此外,仓储实践中发现,粮食会因为热量的积聚使粮堆温度不正常升高,这可能会导致仓储粮堆霉变、变质。为此仓储人员提出将壁面带有小孔的管子插入粮堆内部,提升插管部位附近的空气流速,从而防止该部位粮堆温度的不正常升高。插管上的孔洞,考虑其大小能够防止粮食颗粒进入孔管即可,本实验在CFD模型中使用与通风笼相同的孔板考虑该孔管壁面。对粮堆内风速较小的区域进行插管处理,以期对这些部位的空气流动速度有所提升,通过CFD后处理观察局部风速提升效果,以期解决热量积聚导致的发热、霉变问题。
1.1 k-ε模型
CFD模型计算采用k-ε模型,计算过程中主要求解以下几个方程:
1)连续性方程
(1)
式中u为流体速度。
2)动量方程
(2)
式中ρ为流体密度,t为时间,p为压力,fi为质量力,μ为流体动力粘度。
3)k-ε方程
湍流动能k,与其耗散率ε,由以下输运方程获得
(3)
(4)
式中,k为紊流脉动动能;ε为紊流能量耗散率;υt为紊流粘性系数;
Ck,Cε,C1均为实验常数,这些常数由朗特和斯帕尔汀通过实验、理论分析和经验共同得出,需要指出,k-ε三维紊流数学模型并非根据某种流体的特殊流动状态确定,上述常数根据紊流脉动量的试验和研究成果确定,因此该模型具有广泛的适用性。
1.2 多孔介质模型
多孔介质通过对标准流体流动方程附加动量源项进行模拟,源项由两部分组成:粘性损失项和惯性损失项。源项表示为下式:
(5)
|V|是速度大小,D和C是指定的矩阵。
对于简单各向同性多孔介质
(6)
α是渗透性,C2为惯性阻力系数,D和C是含有1/α和C2的对角矩阵。
1.3 多孔阶跃模型
多孔阶跃模型用于模拟已知空气通过流速和压力损失关系的薄膜,本质是对于多孔模型的一维简化。鉴于该模型的健壮性和更好的收敛性,数值模拟应尽可能地使用这个模型。
薄层多孔介质具有一个有限厚度,其压力降由达西定律和附加惯性损失项定义,压力变化和垂直于多孔面的流速关系由下式给出
Δp=mV2+nV
(7)
其中
这里,C是压力阶跃系数,V是垂直于孔面的速度,Δl是介质厚度,α为渗透性系数。
粮食储藏中使用的通风笼通常是厚度为2 mm的冲孔板(如图1所示),按前述的多孔阶跃模型进行考虑。
测试孔板的流速—压力降特性,按照[8]和[9]中的方法,测试在一定风速下,空气通过孔板的压力降,将每一组风速—压力降数据,以风速为横坐标,压降为纵坐标作图,并拟合为式(7)的形式,通过拟合式中m和n的值来计算渗透性和压力阶跃系数。此类问题可以通过实验解决,也可以通过数值模拟孔板流动压力场、流场解决。本实验采用后者,数值模拟方法获得空气通过孔板的流速和压力降的特性曲线。使用scStream软件对孔板进行建模,通过前期调研,确定了孔板的开孔尺寸,如图2所示。

图1 孔板通风笼
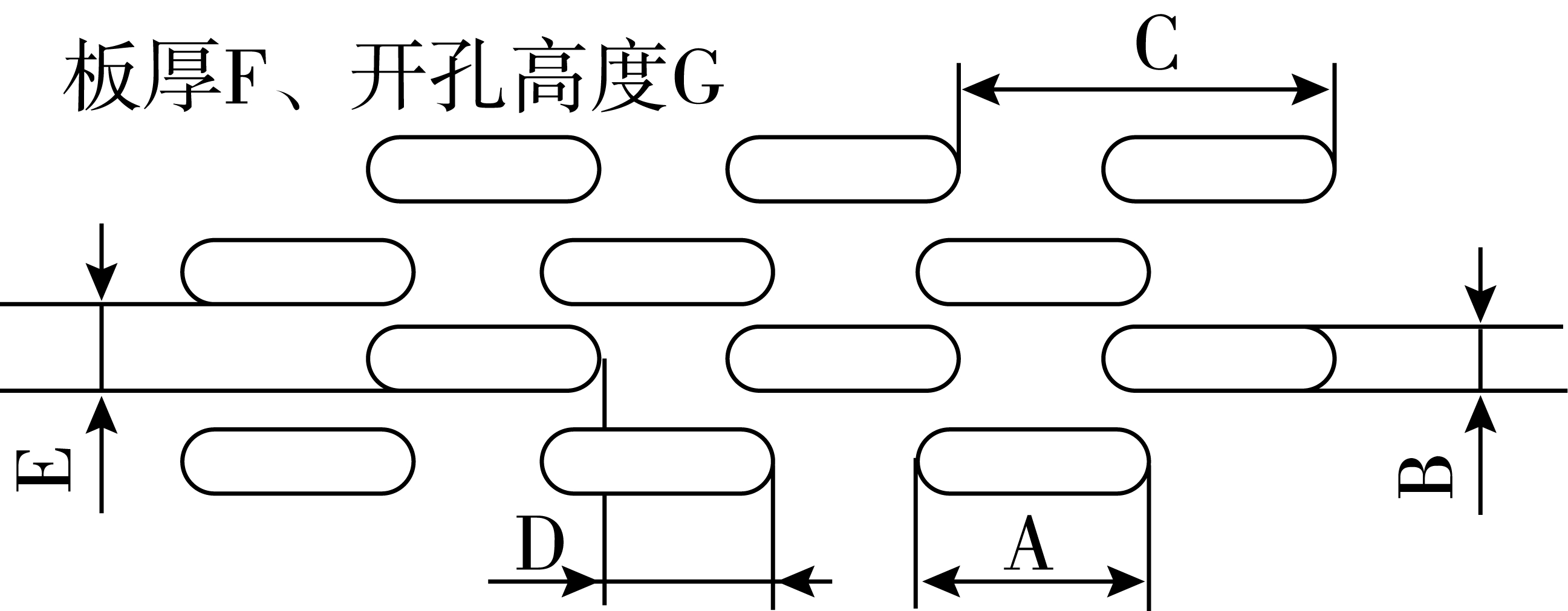
A=20 B=5 C=30 D=15 E=15 F=2 G=0.5
图2 通风笼开孔尺寸(单位:mm)
孔板建模注意到双启桥式开孔高度较小,本实验模拟中开孔高度为0.5 mm,接近实际,使用中须按照孔板加工情况进行设置。采用scStream软件对孔板流动进行模拟,使用k-ε方程计算。划分结构化六面体网格10 160 900个,总体网格尺寸0.5 mm(如图3所示)。

图3 通风笼孔板建模
从孔板模型模拟结果获得流速—压差数据列入表1中:
表1 孔板模拟数据
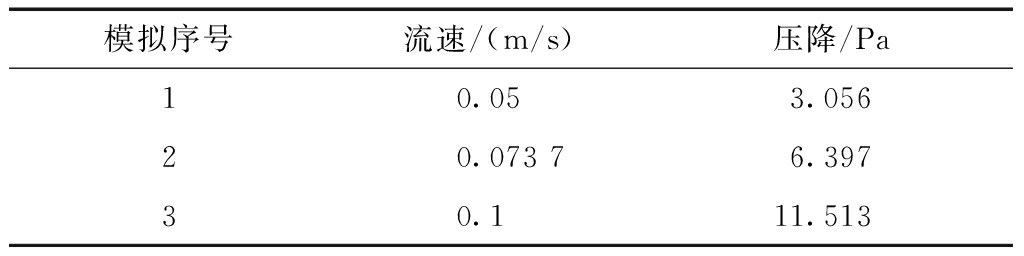
共测试三组实验值用于拟合流速—压降曲线。三组数据两两联立方程组求解m、n的值,同时使用Excel对含有m、n的曲线进行拟合,所得结果列入表2:
表2 m、n求解结果

图4描绘在压力—速度坐标上的数据点和表达曲线,三组数据求解结果相近,取其中比较适中的2、3方程组求解结果,进一步计算式(7)中的参数,即渗透性系数α和压力阶跃系数C,板厚Δl=2 mm已知。求得α=5.132 83×10-9,C=896 952.6。将这两个参数和板厚输入Fluent软件的porous jump边界条件对孔板进行模拟。

图4 拟合曲线和数据点
根据典型平房仓图纸,取一排平房仓中的一榀单独进行模拟。单一粮仓长29.44 m,宽23.5 m,高10.29 m,堆粮高度6 m,粮面以上有通风开口与室外大气连通。送风采用“U”型通风笼,总长度22.705 m,单个通风笼宽0.5 m,共三条,位于地平面上。由两台风机将空气送入通风笼,参考国家粮食储备库使用的两种风机,一种风机风量14 000 m3/h,全压652 Pa;另一种风机风量5 700 m3/h,全压176 Pa。本实验设置每台风机风量10 000 m3/h。
参照实际情况,使用Gambit软件进行建模。为减少网格数量,同时保证网格密度,将通风笼按截面积简化为长方形的通风笼。通风笼网格尺寸0.1 m,采用六面体Hex Submap网格形式。粮食网格尺寸0.1 m,采用六面体Hex Submap网格形式。粮食顶部空气为0.2 m的四面体网格,采用Tet/Hybrid TGrid网格。建模及网格如图5。

图5 建模及网格划分
划分网格数如表3所示。
表3 网格划分数量

送风口大小为0.88 m×0.2 m,按风量折算风速:15.78 m/s。湍流动能:0.392 545 7 kg·m2/s2,湍流耗散率:1.771 474 m2/s3。空气密度1.225 kg/m3,粘度1.789 4×10-5 kg/m·s(按照15 ℃时的值进行计算)。大气压力101 325 Pa。
孔板边界采用porous jump,参数由前述孔板边界确定一节给出。
粮食为多孔介质,分水稻和小麦两种,在Fluent中使用porous media区域类型,参照张忠杰[1]、任广跃[3]的工作,按照密度法测量孔隙度和测量平均颗粒直径的方法获得的阻力参数如表4(不计垂直高度方向粮食孔隙率的变化)。
表4 水稻及小麦阻力参数
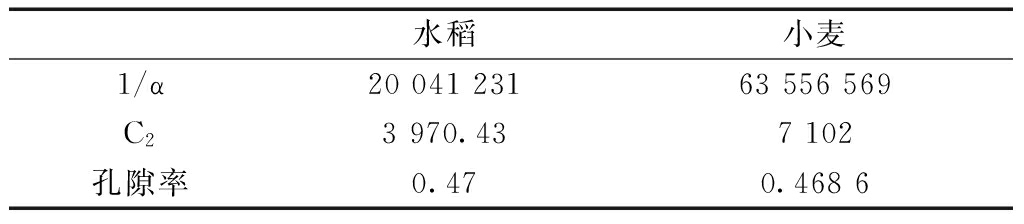
壁面采用无滑移边界条件,粮仓通风窗口设为大气零压力边界条件。
采用CFD模拟软件Fluent进行求解,针对粮仓通风使用该软件求解稳态通风状态下的风速、压力,读取模型中各个点的值生成速度云图或曲线来了解粮堆内部的空气流速和压力分布状况。从而设计粮仓插管通风方案,观察插管对粮仓通风效果的影响。
4.1 通风笼边界的应用对笼内压力的影响
由于本文进行的系列模拟加入通风笼孔板的多孔阶跃边界条件,因此首先对通风笼多孔阶跃边界条件的应用效果进行考察,进行了一组同工况的水稻粮堆通风实验,在相同的送风量,相同的粮堆条件下,考察通风笼孔板处设置压力阶跃边界条件和不设置该边界条件的两种情况下的笼内压力对比。取图5两条中间通风笼的中心线做采样位置,观察线上1 000个采样点的压力值,如图6所示。
分别为左右两个中间通风笼中心线的压力图,随着送风时空气从通风笼的渗出,通风笼中的风速减小,因此静压沿通风笼长度方向逐步增大。两条曲线中上面一条曲线表示通风笼孔板处设置压力阶跃边界条件的模拟结果,下面的曲线则是不含该边界条件的模拟结果。两者相差最大处在通风笼尾部,不含通风笼压力阶跃边界条件的模型压力值低于70 Pa,而将其加入模型后,该处压力大于80 Pa,也就是说不考虑通风笼的压力阶跃,压力误差可达到12.5%。因此,加入孔板通风笼多孔阶跃边界条件有助于真实地体现粮仓内部的空气压力状况,并且在之后的模拟中都考虑孔板通风笼的作用。
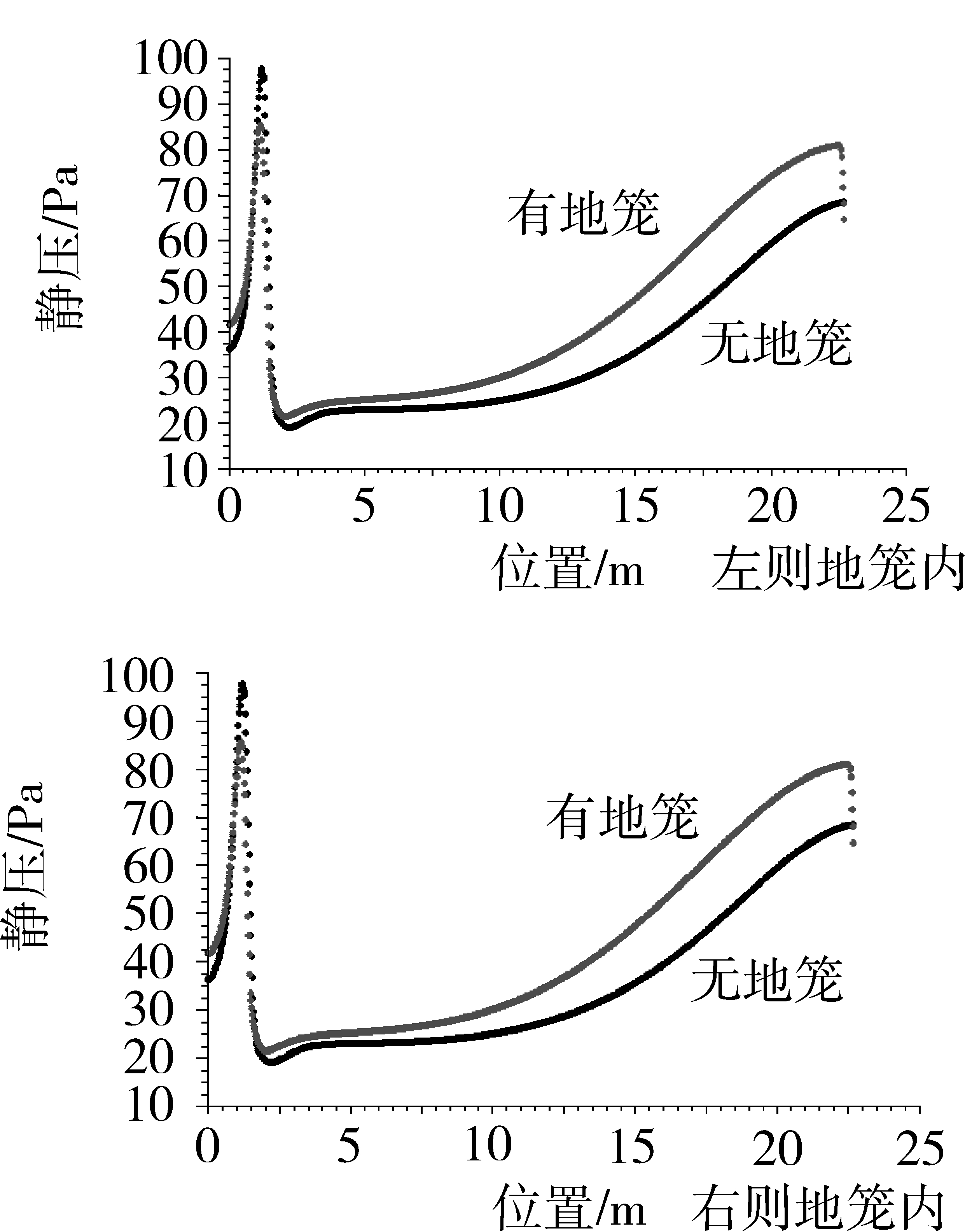
图6 通风笼内压力对比图
4.2 不插管水稻工况
如图7所示,是三个粮堆平面的空气流速云图,可以通过观察发现,平面由下到上,风速均匀性逐渐提升。Z=2的平面最为靠近送风通风笼,存在许多低风速区,中间通风笼上方的空气流速很大,可达到前部的约3倍。

图7 不插管水稻空气流速
粮食插管通风技术可以有效提升粮堆内风速,本文考虑以此对高大平房仓粮堆局部发热进行处理。粮堆内各平面风速高低分布具有相似性,因此按照Z=2平面的风速云图进行插管,来提升风速最低位置的空气流动速度。
参照Z=2平面风速云图,确定插管位置为(X,Y)=(2.4,5.15)(12.1,5.15)(14.8,5.15)(17.4,5.15)(27.1,5.15),并每隔三米插入一排,共三排。为提高中央低风速区的空气流动速度,将(X,Y)=(14.8,5.15)的通风管在每隔三米插入一根的同时,后部再每隔三米插入一根,共三根。总计插入18根通风管。为便于和插管后的情形进行对比,将X=14.8 m处的压力和速度云图(如图8)进行了截取。
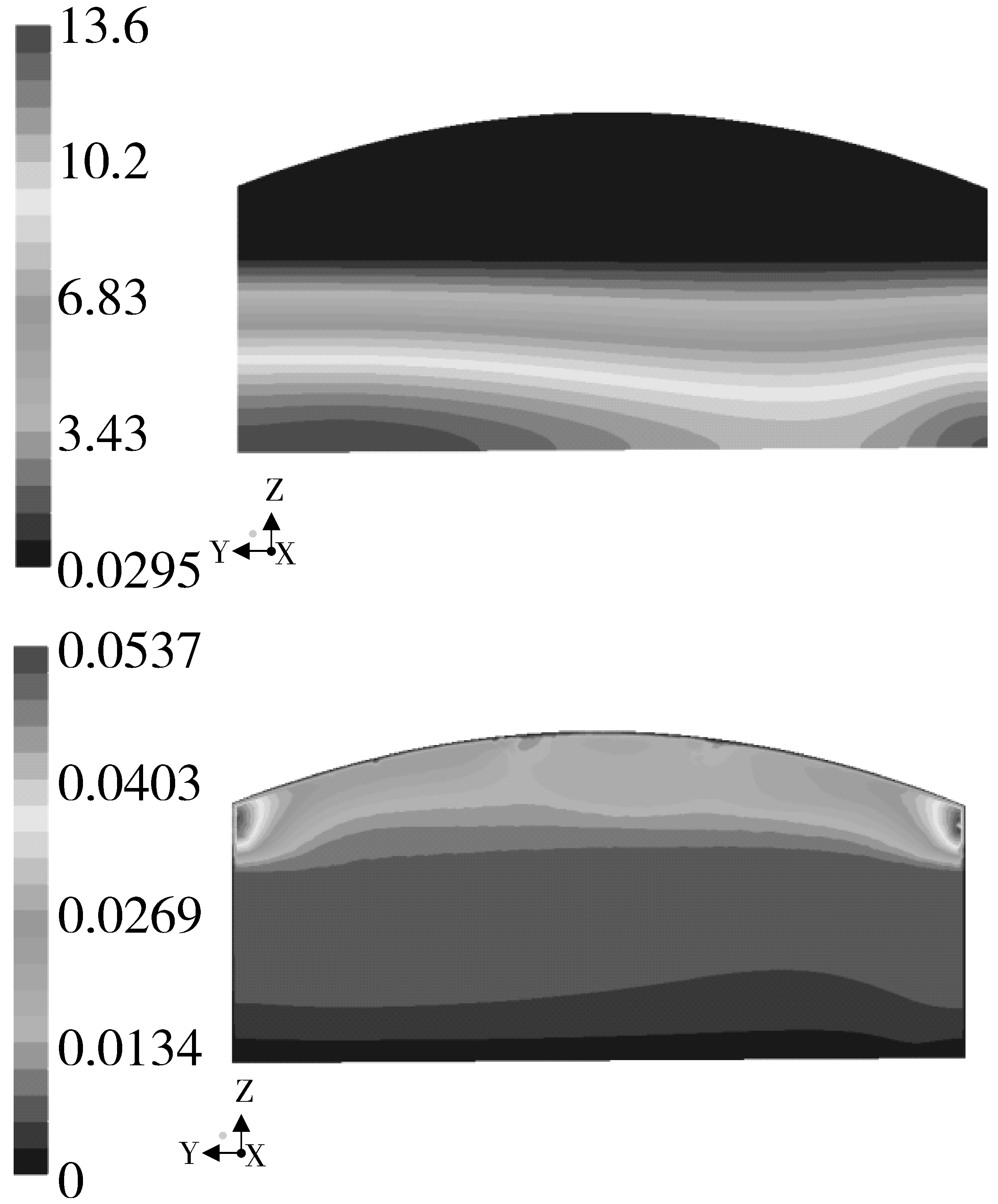
图8 不插管X=14.8平面压力(左)、速度(右)云图
4.3 前三排加中间六根插管水稻工况
通过观察速度云图(图9)发现Z=2平面上的

图9 18根插管空气流速
中部低流速区域已经消失,插管有效提高了粮仓中部“通风死角”部位的风速。而Z=4平面上插管附近风速仍较小,Z=5.9平面上的插管附近风速较大,在Z=2和Z=5.9平面上粮仓前部空气流动速度确有提高,起到了改善局部通风效果的作用。
对比观察插管与不插管工况的压力与风速云图(图10),可以发现插通风管的效果是将低压送入了粮堆内部,由于插管与空气间存在突扩阻力,因此管内压力稍高于粮堆外空气压力。粮堆内部压力由下至上逐步衰减,因此造成这样一个现象:即粮堆内下部压力大,管内空气压力小,空气由粮堆挤入通风管,使通风管底部空气流速较快。随高度增加,粮堆压力与管内压力趋于一致,推动力减小,此时插管管壁附近空气流速小。高度继续增加,插管内空气压力大于附近粮堆压力,空气由通风管进入附近粮堆。
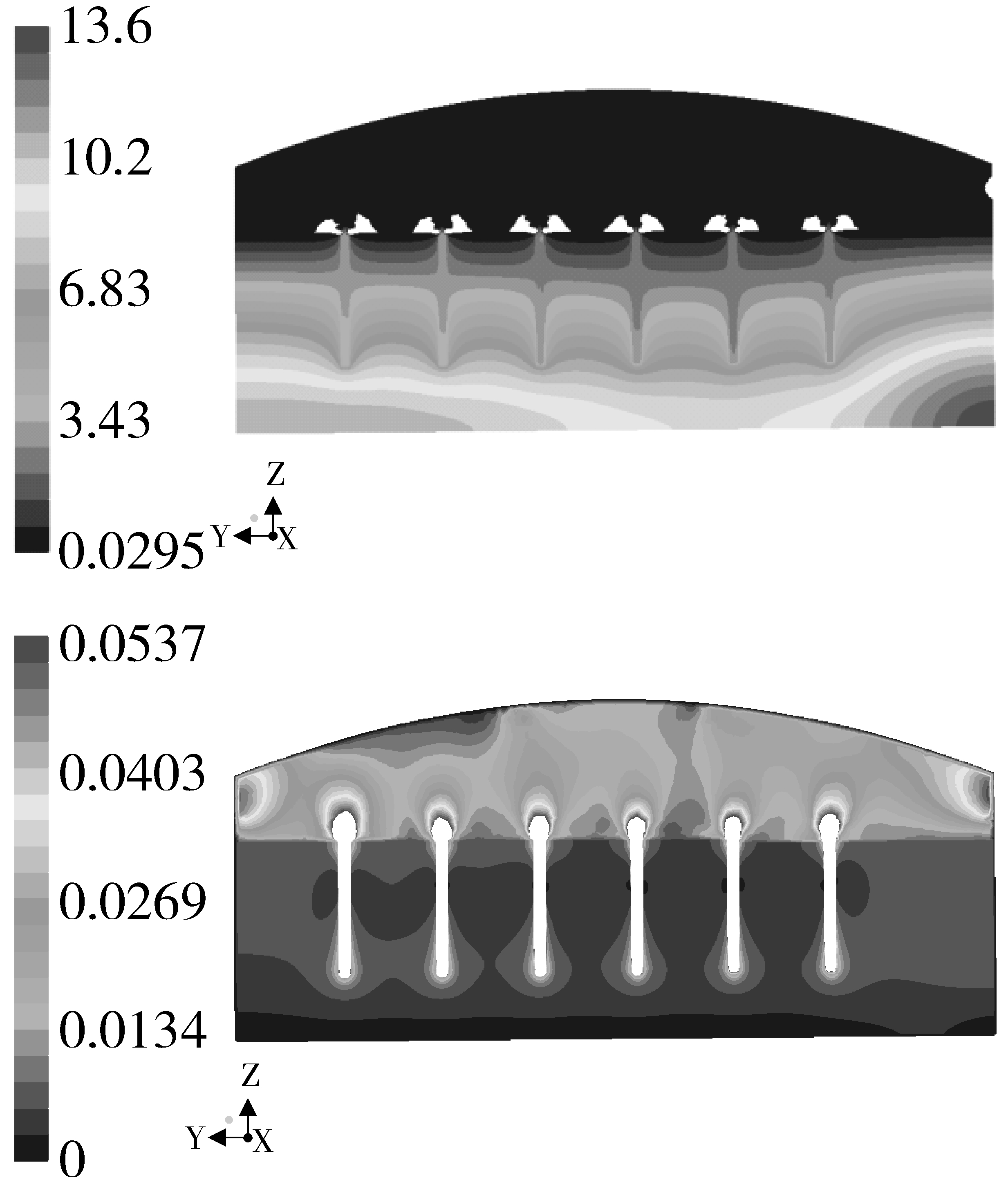
图10 插管X=14.8平面压力(左)、速度(右)云图
经过计算和考察,可以认为插管深度为4 m比较合适。插管太深,易造成通风管与通风笼短路,插管太浅,管内外压差太小,改善效果不大。
为验证插管对风速提升的效果,从模型中读取中间一列六根插管底端下方0.2 m处风速数据,如图11。未插管曲线平均风速0.005 05 m/s,插管后提升至0.007 07 m/s,平均风速提高达到40%,通风效果提升明显。

图11 插管与不插管风速对比图,曲线位置X=14.8 Z=1.8
4.4 不插管小麦工况
与水稻仓储风速进行对比,可以发现在同样的送风量下小麦仓储的情况,空气流速均匀性明显好于水稻仓储时的情况。风速大小的分布与水稻工况相近,因此同样按照水稻5.3节的插管方案对水稻进行插管工况模拟,观察插管对局部风速提升的效果(图12)。

图12 不插管小麦空气流速
图13是通风笼内部中心线的压力数据曲线图,上方线条即小麦的压力数据,显著高于水稻工况,平均相差约60 Pa,即向粮堆进行同样风量的通风,小麦需要更大的压力,即小麦的通风阻力更大。这也使小麦粮堆风速均匀性好于水稻粮堆。

图13 水稻、小麦通风笼内压力对比
4.5 插管小麦工况
同样地,插管提高了Z=2和Z=5.9平面上低空气流速区的空气流速,与水稻工况的模拟结果比较相似(图14)。
图15为中间一列插管压力、风速图(注意颜色标尺有所调整)。与水稻工况相比,小麦粮堆内部压力更大,与管内压差也更大,从管中排风也就更多。流场显示,插管手段提高了管底端和顶端的空气流动速度,但插管中部速度依然较小,需要考虑进一步增加技术手段提高这部分空气流速。

图14 18根插管小麦粮堆空气流速

图15 X=14.8平面压力(左)、速度(右)云图
通过孔板实验数据,将孔板加入整体模型,发现在粮仓中孔板通风笼对压力场存在影响。通风笼内压力,在有孔板通风笼和没有孔板通风笼的两种工况下有相当差距,最大可达到12.5%。
验证插入通风管提升粮堆风速的效果。模拟结果表明,插管可以对管周围的空气流速进行有效提升,管底部平均风速可提升40%,显著改善粮堆局部通风效果,及时排除粮堆内热量,防止粮食发霉、变质。
在孔板通风管底部,管内压力小于附近粮堆压力,空气由粮堆进入通风管。通风管顶部,管内压力大于附近粮堆压力,管内空气向粮堆溢出。这些作用可以显著改善粮堆通风状况。在插管中部,管内外压力相近,粮堆空气流速小,可以就此问题对插管进行细致设计,如改变开孔率,调整管径等。
由于靠近管壁处流动截面小,所以管壁附近空气流速偏大。对此问题可以认为现有插管的型式仍有进一步优化的潜力。
小麦粮堆的通风阻力相对稻谷粮堆较大,因此小麦粮堆相比水稻粮堆能够更好地平衡内部各处空气流速。
参考文献:
[1]张忠杰,李琼,杨德勇,等.准静态仓储粮堆温度场的CFD模拟[J].中国粮油学报,2010(4):46-50.
[2]Yuancheng W,Haifeng D,Haozhang, et al.Modeling on heat and mass transfer in stored wheat during forced cooling ventilation[J].Journal of Thermal Science,2010(2):167-172.
[3]任广跃,彭威,张忠杰,等.仓储粮堆机械通风时压力场的模拟研究[J].中国粮油学报,2012(9):90-95.
[4]彭威.仓储粮堆内部流场CFD模拟研究[D].河南科技大学,2012.
[5]陈桂香,岳龙飞,张虎,林淼达.高大平房仓机械通风量优化数值模拟[J].河南工业大学学报(自然科学版),2014(4):86-90.
[6]陈桂香,岳龙飞,林淼达,张虎.粮堆内热湿耦合传递数值模拟与试验验证[J].中国粮油学报,2014(1):77-82.
[7]张海红.粮库机械通风系统的数值模拟研究[J].粮食科技与经济,2010(3):25-27.
[8]Fluent,Inc.Fluent user’s guide[M].Southpointe:Fluent Inc.,2011.
[9]CFD,Online.Fluent FAQ[EB/OL].http://www.cfd-online.com/Wiki/Fluent_FAQ.●![]()
ZHANG Cheng,FAN Hong-ming
(Beijing University Of Technology,Beijing 100124)
Abstract:The air speed distribution of grain ventilation in horizontal warehouse which is usually concerned is investigated by using CFD numerical simulation.Carefully considered air pressure distribution in the barn.Established independent numerical model for the ventilation cage of the cage ventilation method,obtained its pressure drop versus velocity data,and applied it to the full numerical model of the barn,improved the reality of the simulation.And simulated ventilation tubes in grain heaps based on the tube insertion technology from some barns.It is observed from the test result that air speed in the grain is effectively improved by reasonable arrangement of the ventilation tubes.Proposed the theory of the improvement of the ventilation effect by tube insertion and the direction of optimal designing of the ventilation tube through the observation of the flow field and pressure field nearby ventilation tubes.
Key words:grain ventilation;air speed;CFD;ventilation cage;ventilation tube
收稿日期:2015-09-06
作者简介:张成,1991出生,男,硕士研究生.
中图分类号:TS 379.3
文献标识码:A
文章编号:1007-7561(2016)01-0095-07